- Blood coagulation and thrombosis
- Mathematical modelling of atherosclerosis
- Heart modelling
- Blood flow
- Stroke and patient rehabilitation
Blood coagulation and thrombosis
Following any tissue and blood vessel injury, excessive blood loss is prevented by activation of hemostatic mechanisms that cause blood plasma to coagulate and platelets to aggregate. This physiological process of clotting performs a vital protective role. However, hemostatic system can also be activated inappropriately leading to blood clot formation within the circulation, a dangerous thrombosis scenario that is the key trigger for heart attacks and strokes. Thromboses and bleedings are the leading cause of death in many diseases and conditions such as atherosclerosis, myocardial infarction, stroke, sepsis, cancer, snakebites, frostbites, burns, surgery, as well as hemophilias and other inherited and acquired diseases.
In order to be able to function appropriately under various life challenging conditions, hemostasis has evolutionary evolved into the exquisitely complex system. It incorporates two interdependent mechanisms, one mediated by blood cells known as platelets which aggregate at the site of vessel damage (cell hemostasis, or platelet hemostasis), and the second mediated by complex biochemical cascade controlling the formation of a polymer fibrin mesh (coagulation, or plasma hemostasis). Thus, hemostasis function encompasses processes of various physics, biochemistry, and time/space scales: non-Newtonian hydromechanics; fluid-to-gel transformations; cell adhesion and shape change, platelet contraction; intricate complex intra- and extra-cellular biochemical reaction networks. All together they possess complex spatiotemporal response dynamics. To study these problems, we apply comprehensive theoretical and computational methods and approaches.
Thrombin generation
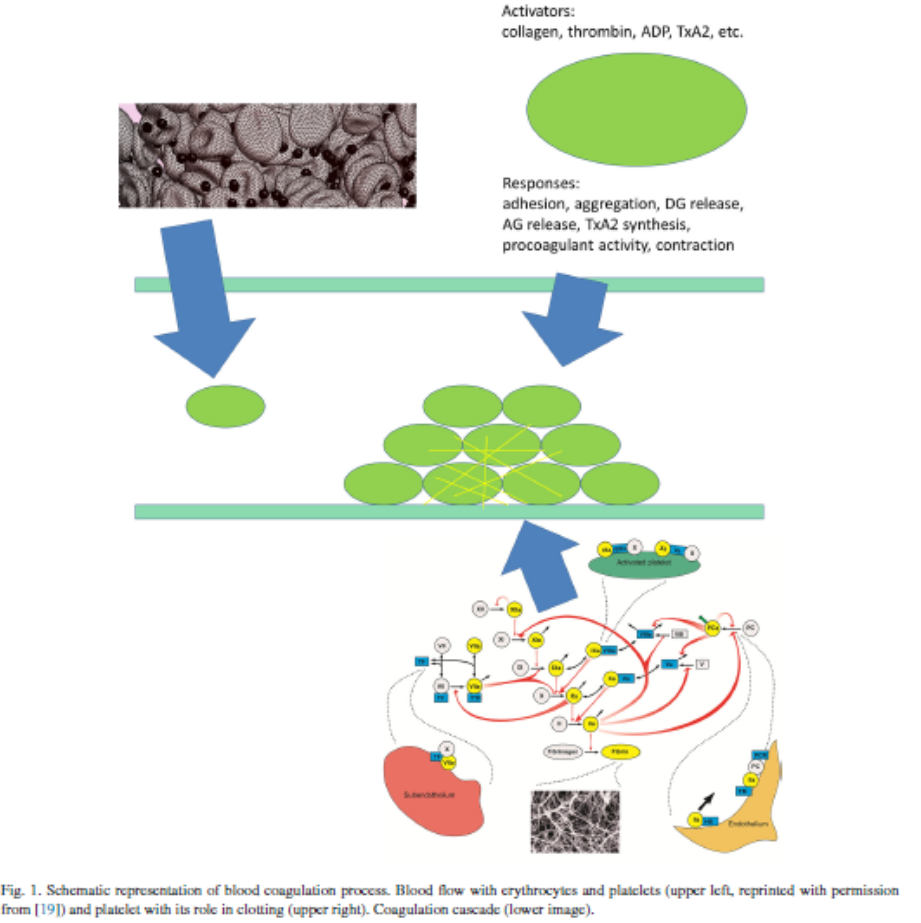
The primary function of the coagulation system is the termination of bleeding caused by vessel wall damage. This is achieved by covering the injured site with a fibrin clot that appears at the final stage of a complex proteolytic enzymatic cascade where activated clotting factors act as catalysts for activation of others [53,54]. The key enzyme of this coagulation cascade is thrombin (Fig.1), it uniquely catalyses the conversion of fibrinogen to fibrin as well as playing a crucial role in controlling the kinetics of clot formation [53,55,56]. Thrombin formation can be launched by tissue damage that ruptures the endothelium exposing tissue factor to blood flow (this is called the extrinsic pathway), or by contact with a foreign substance where activation of factor XII triggers activation of factor XI (this is called theintrinsic pathway) [54,57,58]. Both pathways lead to the activation of factor X that contributes to the conversion of prothrombin to thrombin [54]. Once thrombin concentration reaches a threshold value, further prothrombin activation takes place due to positive feedback loops within the coagulation cascade [54,57,40].
There are numerous works devoted to modeling the coagulation cascade under different simplifying assumptions, these are necessary since the complete reaction scheme is complex and not completely known, especially if platelets are involved. In vitro coagulation kinetics through the extrinsic pathway were modeled in [59–63]and through the intrinsic pathway in [64–67]. All of these models exclude platelets, their influence being taken into account in [68–71]. In vivo coagulation kinetics is studied in [72–77]. These models all vary in the number of reactions (from 12 to 93), concentrations (from 6 to 92) and parameters (from 16 to 48) included, reflecting the simplifying assumptions underpinning their construction.
Clot growth as a reaction-diffusion wave
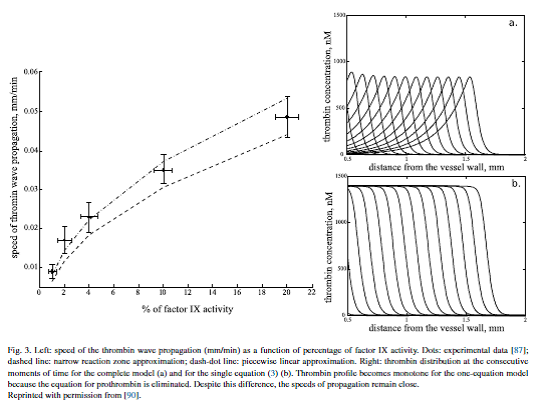
Having investigated the coagulation cascade utilizingordinary differential equations we now increase complexity by taking into account the diffusion of blood factors in plasma. The resulting reaction–diffusion system describes clot growth and emits travelingwave solutions. The concept of clot growth as a reaction–diffusion wave was introduced in the 1990s [84,81,66]starting an intensive investigation of wave dynamics and properties [82,85–88]. The main questions here are the determination of the conditions of wave initiation, the speed of its propagation and the mechanisms of its arrest. From a physiological point of view these determine the clot size and differentiate normal, hemophilic and thrombotic plasma. In particular, low wave speed is specific for hemophilic patients while large wave speed can result in thrombosis.
Blood coagulation in flow
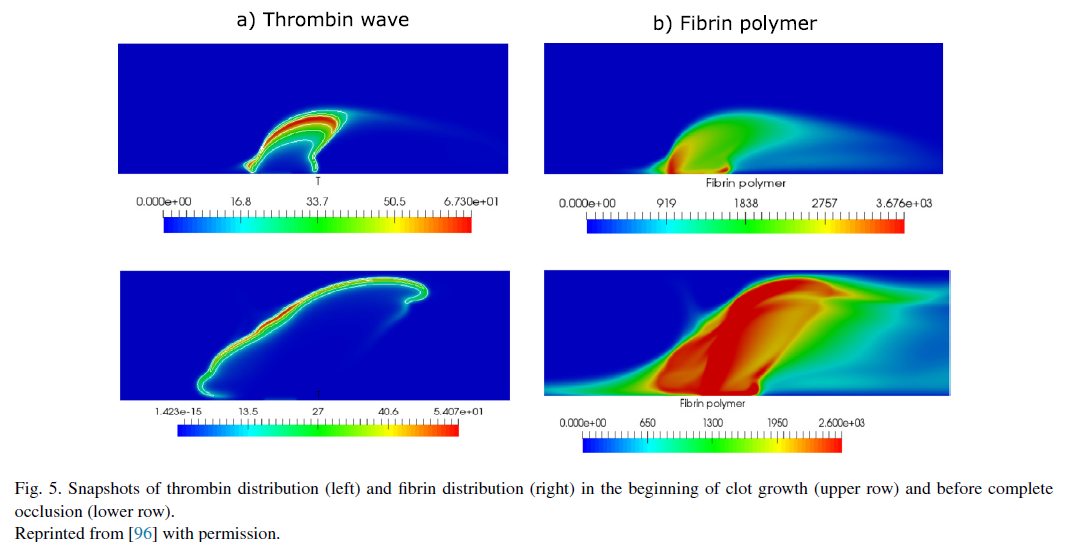
Increasing the complexity of the model we now introduce blood flow, excluding the influence of blood cells, which will be considered in the following sections. Blood flow brings inactive blood factors, such as prothrombin or fibrinogen to the clot and removes active factors, including thrombin, from the clot. Conditions of clot initiation in flow and the distributions of blood factors during clot growth are studied in several works [97–101]and include comparisons with experiments undertaken in flow chambers [102,103]. Coagulation with non-Newtonian flow is studied in [104–106].
* Text, figures and references are taken from [1]
Blood coagulation with platelets (in images)

Platelet motion near the wall (courtesy A. Belyaev)
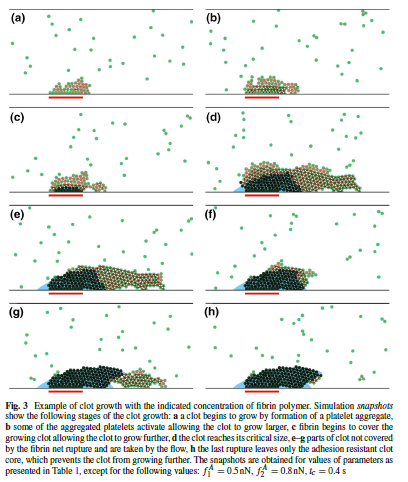
(from [7])
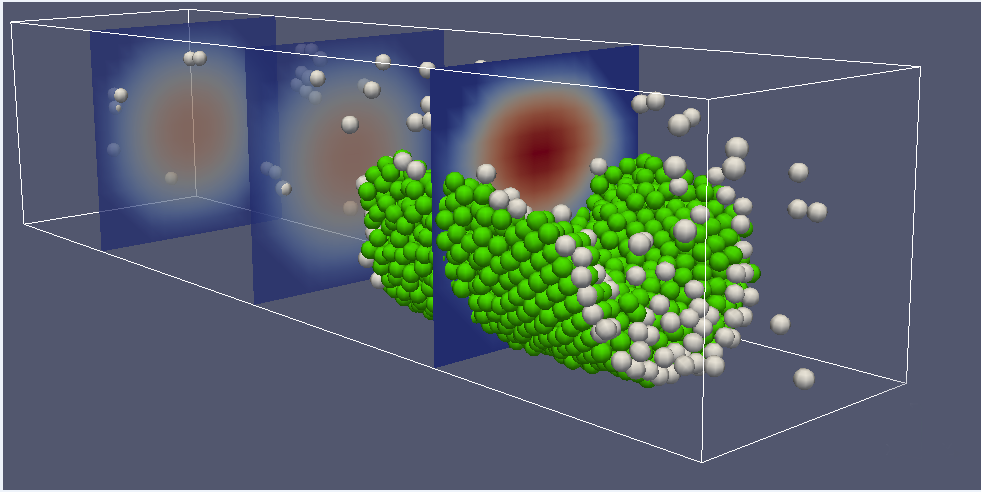
Platelet aggregation (courtesy A. Belyaev)
Hemostasis and thrombosis in aneurysms and complex geometries
If the walls of the blood vessels are damaged after trauma, inflammation or rupture of the arteriosclerotic plaque, the process of thrombus formation starts. Normally, this phenomenon, called hemostasis, is designed to stop bleeding and is a protective mechanism. However, in some cases, this mechanism fails, the result can be a blockage of the blood vessels by a severed thrombus and other life-threatening conditions, for example, heart attacks and strokes. Not all mechanisms of regulation of thrombosis have been well-studied due to the biophysical complexity of the process, but it has been established that the geometry of the vessels and the hydrodynamic properties of the blood flow can play a role in the growth of thrombus. However, the structure of the microvascular bed is specific for each individual patient. The doctors are faced with the task of identifying the risks associated with safety, or a dangerous thrombus. The creation of a numerical personalized model of thrombus growth in each case would help in making these decisions in the treatment and prevention of thrombosis. The goal of this project is to create and verify a predictive three-dimensional computer model of thrombus growth in arterioles and venules for personalized medicine. The project proposes a combination of technologies of modern highly effective numerical methods for modeling blood mechanics (hemodynamics) with a systemic biophysical model of blood coagulation and aggregation of blood platelets. A combined model of biochemical plasma clotting reactions with a three-dimensional hemodynamic model is planned for the first time. Verification of the method will be based on comparable results in the available in the literature experimental material on the growth of thrombus in vivo. With the help of numerical models, depending on the geometry of the vessels, the size and shape in each of the levels: growth and severance of thrombus in the arterioles, growth of thrombus in stagnant areas (in aneurysms), the formation of a hemostatic plug in the open wound.
Publications
- Belyaev, A.V., Dunster, J.L., Gibbins, J.M., Panteleev, M.A., Volpert, V. Modeling thrombosis in silico: Frontiers, challenges, unresolved problems and milestones. Physics of LifeReviews, 2018, v. 26-27, pp. 57-95.
- A. Bouchnita, T. Galochkina, P. Kurbatova, P. Nony, V. Volpert. Conditions of microvessel occlusion for blood coagulation in flow. International Journal for Numerical Methods in Biomedical Engineering, 2017, e2850.
- A. Bouchnita, K. Bouzaachane, T. Galochkina, P. Kurbatova, P. Nony, V. Volpert. An individualized blood coagulation model to predict INR therapeutic range during warfarin treatment. Math. Model, Nat. Phenom, 11 (2016), no. 6, 28-44.
- A. Bouchnita, T. Galochkina, V. Volpert. Influence of antithrombin on the regimes of blood coagulation: insights from the mathematical model. Acta Biotheoretica, 64 (2016), 64, no.4, 327-342.
- T. Galochkina, H. Ouzzane, A. Bouchnita, V. Volpert. Traveling wave solutions in the mathematical model of blood coagulation. Applicable Analysis, 96 (2017), no. 16, 2891-2905.
- A. Bouchnita, A. Tosenberger, V. Volpert. On the regimes of blood coagulation. Applied Mathematics Letters, 51 (2016) 7479.
- A Tosenberger, F Ataullakhanov, N Bessonov, M Panteleev, A Tokarev, V Volpert. Modelling of platelet-fibrin clot formation in flow with a DPD-PDE method. Journal of Math. Biology, 72 (2016), no. 3, 649-681.
- A. Tosenberger, N. Bessonov, V. Volpert. Influence of Fibrinogen Deficiency on ClotFormation in Flow by Hybrid Model. Math. Model. Nat. Phenom., 10 (2015) No. 1, 36-47.
- A. Tosenberger, F. Ataullakhanov, N. Bessonov, M. Panteleev, A. Tokarev, V. Volpert. Modelling of thrombus growth in flow with a DPD-PDE method. Journal of Theoretical Biology, 337 (2013), 30-41.
- A. Tosenberger, F. Ataullakhanov, N. Bessonov, M. Panteleev, A. Tokarev, V. Volpert. Modelling of thrombus growth and growth stop in flow by the method of dissipative particle dynamics. Russian Journal of Numerical Analysis and Mathematical Modelling" 2012, Vol. 27, No. 5, 507-522.
- A. Tokarev, I. Sirakov, G. Panasenko, V. Volpert, E. Shnol, A. Butylin, and F. Ataullakhanov. Continuous Mathematical Model of Platelet Thrombus Formation in Blood Flow. Russian Journal of Numerical Analysis and Mathematical Modelling. 2012, Vol. 27, No. 2, pp.192-212.
- A.A. Tokarev, Yu.V. Krasotkina, M.V. Ovanesov, M.A. Panteleev, M.A. Azhigirova, V.A. Volpert, F.I. Ataullakhanov, A.A. Butilin. Spatial dynamics of contact-activated fibrin clot formation in vitro and in silico in haemophilia B: effects of severity and Ahemphil B treatment. Math. Model. Nat. Phenom , 1 (2006), No. 2, 124-137.
- A.V. Belyaev. Catching platelets from the bloodflow: the role of the conformation of von Willebrand factor. Math. Model. Nat. Phenom., 2018, 13 (5): 44.
- A.V. Belyaev. Long ligands reinforce biological adhesion under shear flow. Phys.Rev.E, 97 (4): 042407 (2018).
- Belyaev A.V., Dunster J.L., Gibbins J.M., Panteleev M.A., Volpert V. Advancing research on blood coagulation and thrombosis. Physics of Life Reviews, 2018, v.26-27, pp. 116-119.
- A.V.Belyaev. Hydrodynamic repulsion of spheroidal microparticles from micro-rough surfaces. PLoS ONE, 2017, 12(8), e0183093.
- A.V.Belyaev, M.A.Panteleev and F.I. Ataullakhanov, Threshold of Microvascular Occlusion: Injury Size Defines the Thrombosis Scenario. Biophysical Journal, 2015, v. 109, pp. 450-456 (2015).
- A. Tokarev, N. Ratto, V. Volpert. Mathematical modeling of thrombin generation and wave propagation: from simple to complex models and backwards. Proceedings of the BIOMAT International Symposium on Mathematical and Computational Biology, 2018.
Mathematical modelling of atherosclerosis
High plasma concentration of low-density lipoprotein (LDL) cholesterol is one of the principal risk factors for atherosclerosis. Its mechanism can be sketched as follows: the process of atherosclerosis begins when LDLs penetrate into the intima of the arterial wall where they are oxidized. Oxidized LDL (ox-LDL) in the intima is considered by the immune system as a dangerous substance, hence an immune response is launched: chemoattractants (which mediate the adhesion of the monocytes to the endothelium and the penetration of the monocytes through the endothelium) are released and endothelial cells are activated so that monocytes circulating in the blood adhere to the endothelium and then they penetrate to the arterial intima. Once in the intima, these monocytes are converted into macrophages.
The macrophages phagocytose the ox-LDL but this eventually transform them into foam cells (lipid-laden cells) which in turn have to be removed by the immune system. In the same time, they set up a chronic inflammatory reaction (auto-amplification phenomenon): they secrete pro-inflammatory cytokines (TNF-alpha, IL-1) which increase endothelial cells activation, promote the recruitment of new monocytes and support the production of new pro-inflammatory cytokines.
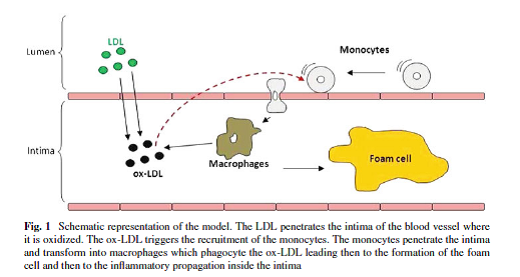
(from [2])
This auto-amplification phenomenon is compensated by an anti-inflammatory phenomenon mediated by the anti-inflammatory cytokines (IL-10) which inhibit the production of pro-inflammatory cytokines (biochemical anti-inflammation). Next, the inflammation process involves the proliferation and the migration of smooth muscle cells to create a fibrous cap over the lipid deposit which isolates this deposit center from the blood flow (mechanical anti-inflammation).
This mechanical inhibition of the inflammation may become a part of the disease process. Indeed, the fibrous cap changes the geometry of the vasculature and modifies the blood flow. The interaction between the flow and the cap may lead to a thrombus, or to the degradation and rupture of the plaque liberating dangerous solid parts in the flow. At low LDL concentrations the auto-amplification phenomenon does not set up and no chronic inflammatory reaction occurs. At intermediate concentrations a perturbation of the non-inflammatory state may lead to the chronic inflammation, but it has to overcome a threshold for that. Otherwise the system returns to the disease-free state. At large LDL concentrations, even a small perturbation of the non-inflammatory state leads to the chronic inflammatory reaction.
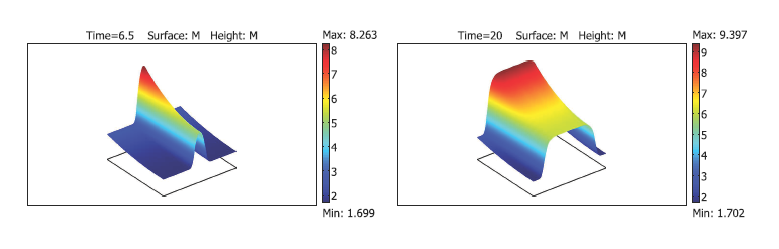
Fig. 2. Chronic inflammation in the blood vessel wall propagates as a reaction-diffusion wave (from [4]).

Fig. 3. Cellular automata modelling of atherosclerosis (from [6]).
Publications
- N. Apreutesei, V. Volpert. Travelling waves for reaction-diffusion problems with nonlinear boundary conditions. Application to a model of atherosclerosis. Pure and Applied Funct. Analysis, Volume 3, Number 1, 43-56, 2018.
- N. El Khatib, S. Genieys, B. Kazmierczak, V. Volpert. Reaction-Diffusion Model of Atherosclerosis Development. J. Math. Biol., 65 (2012), no. 2, 349-374.
- N. El Khatib, S. Genieys, A. M. Zine, V. Volpert. Non-Newtonian effects in a fluid-structure interaction model for atherosclerosis, Journal Techn. Physics, 50 (2009), No. 1, 3-12.
- N. El Khatib, S. Genieys, B. Kazmierczak, V. Volpert. Mathematical modelling of atherosclerosis as an inflammatory disease Phil. Trans. R. Soc. A December 13, 2009 367:4877- 4886.
- N. El Khatib, S. Genieys, V. Volpert. Atherosclerosis initiation modeled as an inflammatory process. MMNP, 2007, No. 2, 126-141.
- R.N. Postona, D.R.M. Poston. Typical atherosclerotic plaque morphology produced in silico by an atherogenesis model based on self-perpetuating propagating macrophage recruitment. Math. Model. Nat. Phenom, Vol. 2, No. 2, 2007, pp. 142-149.
Introduction
Detailed multiscale models of the heart within cardiovascular systems could be very useful in a diagnosis and treatment of heart diseases. The models of that type combine the descriptions of the electromechanics of a cardiac cell, myocardium tissue, heart geometry and vascular bed. Such models could include patient-specific approximation of the heart geometry and orientation of muscle fibres allowing numerical investigation of the effects of local dysfunctions of myocardium mechanics or electromechanics along with accompanying remodelling of the ventricular and atrial walls.
Our study
In our study we have developed a new model of myocardium mechanics that set relationships between macroscopic muscle stress and strain and the variables that specified the states of the contractile and regulatory proteins at the level of a single cell. Being set by a system of ordinary differential equations, this model reproduce a large set of uniaxial experiments performed on single skeletal and cardiac muscle fibres, including such important effects as length-dependent activation of the muscle and load-dependent relaxation. A new lumped parameter model was developed to describe other heart chambers and the vascular bed. The cell model was applied to an axisymmetric approximation of the left ventricle of the heart; along with a new lumped parameter model of the CVS, it was used for the simulation of the heart performance at different conditions.
Results
The results of the simulation of a hear-beat with model parameters corresponding to a healthy human heart showed agreement of the main haemodynamic variables with clinical data, including end-systolic and end-diastolic values of the pressure and volumes of the heart chambers, ventricular and atrial stroke volumes and ejection fractions. Not only radial and axial strains of the whole axisymmetric left ventricle, but also some local strains in different regions of ventricular wall agreed with observations. The effects of some arrhythmias and the stenosis and insufficiency of the aortic and mitral valves on the haemodynamic variables were simulated. In particular, we observed a decrease in the ventricular stroke volume in the cases of asynchronous contraction of the atria and ventricles. The severity of this dysfunction increased in the simulation of a heart-beat at physical exercises, when a heart beat rate increased. We have performed systematic numerical investigation of the stenosis and regurgitation of the aortic and mitral valves and have compared the characteristic variables of such simulations with medical guides for the classification of severity of the examined pathologies. The comparison have shown a good quantitative agreement of our results and the data from the classification guides.
Our current research is focused on the development of a 3D model of the heart including a complete electromechanical model of the myocardium within the cardiovascular system. Such model could be used for the investigation of effects of local heart tissue electromechanical disorders on the heart performance in medical practice. With further development, the model could be used for a decision making in surgery.