Самоорганизация – проще, чем кажется
Явление самоорганизации определило все переходные моменты в истории нашего мира, начиная с самого рождения Вселенной: формирование первых атомов, звезд, планет, жизни, человеческого общества. Всеобщность этого явления делает его очень важным для научного исследования, однако необходимость междисциплинарного подхода препятствовала ему вплоть до середины прошлого века. Одной из первых работ в области самоорганизации стало исследование Алана Тьюринга, широко известного за свой вклад в математику, информатику и искусственный интеллект. В своей работе Алан Тьюринг предположил, что ключом к многим явлениям морфогенеза, то есть формирования органов у живых организмов, является неустойчивость пространственно-однородного состояния в системе диффундирующих по ткани и взаимодействующих друг с другом химических веществ, локальная концентрация которых влияет на поведение клеток, составляющих эту ткань. Такая неустойчивость может приводить к неоднородному распределению этих веществ и следовательно – к разному поведению клеток на разных участках ткани. По такому механизму, согласно гипотезе Тьюринга, у живых организмов на заданном расстоянии друг от друга могут образовываться щупальца, листья и другие органы. Кроме того, узоры на шкурах животных могут формироваться по аналогичному принципу. Поначалу гипотеза Тьюринга не принималась научным сообществом всерьез, но впоследствии она нашла широкое применение во множестве исследований не только биологических, но и физических, химических и даже социологических систем, в которых ключевыми процессами являются локальное взаимодействие элементов и их случайное передвижение в пространстве.

Структуры Тьюринга, впервые полученные в химическом эксперименте.
Алан Тьюринг вывел условия для образования стационарных структур в системах, состоящих из двух взаимодействующих элементов. Согласно им, один из элементов должен быть самоактиватором, увеличение концентрации которого стимулирует его собственное производство. Второй вид должен быть самоингибитором, действующим противоположным образом. Кроме того, подвижность – или коэффициент диффузии – самоингибитора должна быть достаточно выше, чем у самоактиватора – насколько именно, зависит от конкретных значений остальных параметров системы, которые определяют скорости реакций веществ и называются кинетическими. Эти условия составляют концепцию «короткодействующей активации и дальнодействующего ингибирования» (КАДИ). В дальнейшем эта концепция стала общепринятой и для систем с произвольным числом переменных. Основным ее недостатком является то, что, согласно ей, структуры Тьюринга могут возникать в значительном диапазоне кинетических параметров системы, только если подвижности переменных сильно различаются. При этом для химических и биологических систем это, как правило, не так – например, коэффициенты диффузии абсолютного большинства белков в животной ткани различаются не более, чем в несколько раз, что оставляет лишь узкое окно для значений кинетических параметров, при которых могут формироваться структуры. Эта черта является основным объектом критики теории Тьюринга – ведь в биологии, как правило, значения кинетических параметров варьируются в широких пределах как для разных особей, так и для разных участков ткани одной особи, а также просто со временем. Таким образом, с первого взгляда механизм, предложенный Тьюрингом, не является стабильным – то есть незначительное случайное изменение параметров модели запросто может привести к прекращению формирования структур – и в результате животное не получит необходимых ему органов или останется без узоров на шкуре.
Известным приемом, позволяющим значительно повысить стабильность механизма Тьюринга, является обратимое связывание вещества-самоактиватора с третьим, неподвижным, элементом, благодаря чему его эффективная подвижность может быть существенно замедлена. Благодаря этому методу структуры Тьюринга впервые были получены искусственно в 1990 году. Тем не менее, этот прием также вписывается в концепцию КАДИ. Однако в последние годы появились свидетельства того, что в многокомпонентных системах структуры Тьюринга могут формироваться и в обход общепринятой концепции. В частности, было продемонстрировано существование систем с одним неподвижным элементом, в которых структуры Тьюринга возникают при любых коэффициентах диффузии подвижных элементов. Сотрудники нашего Центра «Математическое моделирование в биомедицине» Максим Кузнецов и Андрей Полежаев занялись исследованием этого явления и впервые вывели общие условия, при которых системы обладают данным свойством.
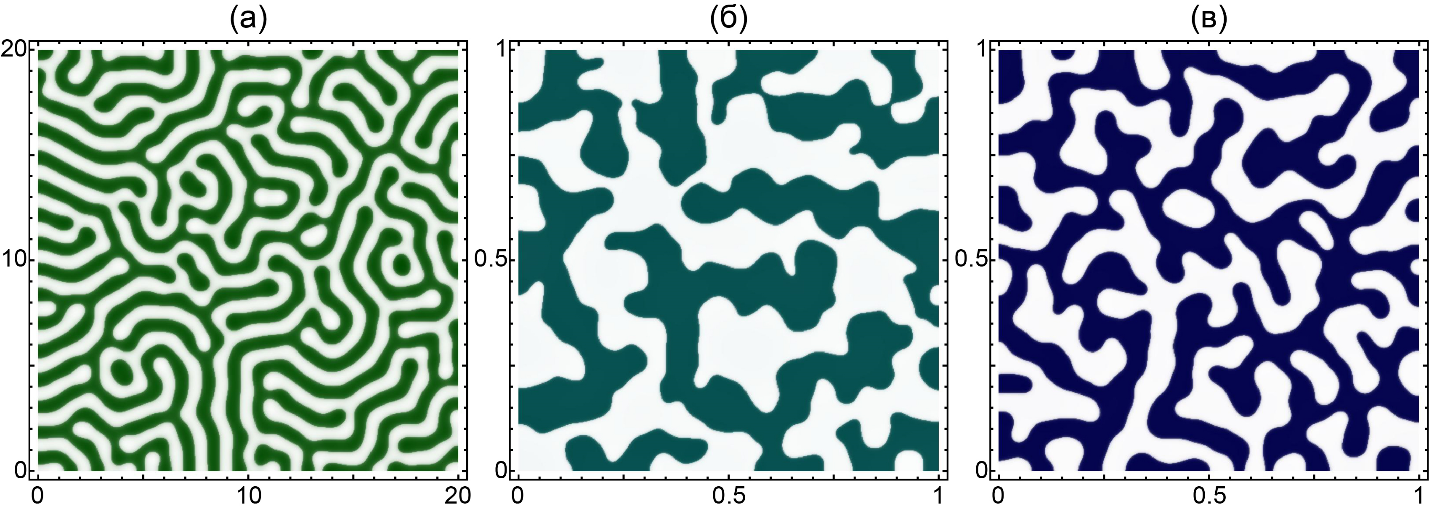
Структуры Тьюринга, возникающие при математическом моделировании трехкомпонентной системы с одним неподвижным элементом, при отношениях подвижностей двух других элементов: (а) 1; (б) 1000; (в) 0,001.
Оказалось, что при наличии в системе неподвижного элемента, не влияющего напрямую на собственное производство – то есть, не являющегося ни самоактиватором, ни самоингибитором – условия для формирования структур Тьюринга качественно изменяются. Особо любопытно, что при этом ключевую роль начинает играть схема типов взаимодействий этого элемента с двумя подвижными элементами. Под типом взаимодействия подразумевается один из трех случаев, в которых увеличение концентрации одного элемента: 1) стимулирует производство другого, 2) ингибирует его или 3) не влияет на него. Исследование, проведенное нашими сотрудниками, показало, что, при определенных схемах типах взаимодействий элементов в системе, структуры Тьюринга формируются в ней не только при любых коэффициентах диффузии подвижных элементов, но и при любых значениях кинетических параметров системы (по крайней мере, если в отсутствие диффузии система оказывается устойчива – иначе происходит борьба разных типов неустойчивостей, которая может приводить к разным результатам). Такие условия предлагают несколько более сложный, но гораздо более стабильный механизм формирования структур Тьюринга по сравнению с классическим – в то время как скорости реакций в биологии могут варьироваться в очень широких пределах, тип влияния одного элемента на другой обычно четко задан.
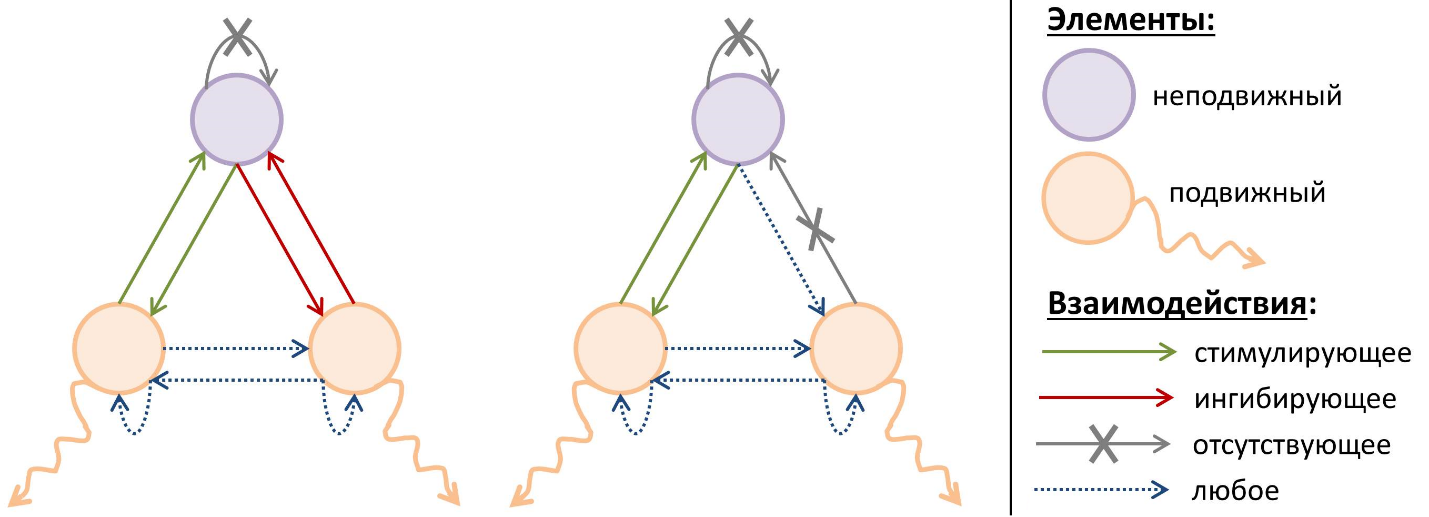
Примеры схем взаимодействий элементов, при которых неустойчивость Тьюринга проявляется при любых значениях параметров системы.
На данный момент неизвестно, реализуется ли такой механизм в живой природе, однако никакое из его условий не противоречит биологическим законам. Более того, так как развитие живого мира диктуется законами биологической эволюции, высокая стабильность найденного механизма должна обеспечить его распространение в природе при условии возможности его реализации. При этом необходимость наличия неподвижного элемента, взаимодействующего с подвижными, подчеркивает важность роли, которую в морфогенезе могут играть клеточные рецепторы, внутриклеточные сигнальные пути и другие элементы, связанные с неподвижными клетками, которые, как правило, игнорируются в математических моделях.
Подробнее об исследовании наших сотрудников можно будет прочесть в статье, на данный момент находящейся на этапе рецензирования в одном из ведущих физических журналов мира.