International online workshop "Mathematical Modelling in Biomedicine"
October 25 – 29, 2021 Moscow, Russia
Organizers
Russia: RUDN University, Moscow State University
France: University of Lyon
Sponsors
RUDN University
Participants
About 50 participants from 10 countries
Platform
MS-Teams
Official Language
English
Registration Fee
No
Sections
∙ Cardiac modelling ∙ Physiology and modelling
∙ Biomolecular modelling ∙ Cancer
∙ Epidemiology ∙ Immunology
∙ Biological fluids ∙ Mathematical methods and analysis
Scientific Committee
A. Panfilov (Co-chairman, Ghent), V. Volpert (Co-chairman, Lyon), G. Panasenko (Lyon), A. Sequeira (Lisbon)
Organizing Committee
V. Volpert (chairman), C. Leon, A. Mozokhina, D. Nechipurenko, A. Tokarev, N. Rodin, L. Proshutinskaya
Confirmed Plenary Speakers
Gennady Bocharov, Yuri Vassilevksi, Jean Clairambault, Andrei Tsaturyan, Mostafa Adimy, Adelia Sequeira, Dmitri Fedosov, Laurent Pujo-Menjouet, Grigory Panasenko, Alexandre Chupakhin
Conference proceedings
– electronic version only
Contacts
Scientific topics: This email address is being protected from spambots. You need JavaScript enabled to view it.
Technical topics: This email address is being protected from spambots. You need JavaScript enabled to view it.
Official registration
- Hits: 1090
International online workshop
Mathematical Modelling in Biomedicine
October 25 – 29, 2021 Moscow, Russia
...to be filled...
- Hits: 382
Математическое моделирование поможет победить рак
Из-за онкологических заболеваний ежегодно умирает около десяти миллионов человек. Разработка эффективных методов лечения рака является для современной медицины важнейшей, но крайне трудной задачей, из-за сложности и невероятного разнообразия злокачественных опухолей. Мы часто слышим в новостях об открытии новых методов лечения рака, но каждый из них слабо доступен широким массам из-за своей дороговизны, и кроме того, каждый из них направлен лишь на узкий круг онкологических заболеваний и имеет ограниченную эффективность. К примеру, успех нового метода из области иммунотерапии, авторам которого в прошлом году была присуждена Нобелевская премия, заключается в значительном уменьшении объема опухолей (не всегда означающем полное выздоровление) лишь у примерно трети пациентов с меланомой и раком почки.
Это означает, что классические методы лечения – такие, как химиотерапия и радиотерапия – будут востребованы еще долгое время. Поэтому важную роль в онкологии играет поиск комбинаций классических видов терапии с высокой итоговой противоопухолевой эффективностью, решающее влияние на которую оказывает расписание введения препаратов или совершения других медицинских действий. Формально для такого поиска требуется проведение колоссального количества клинических испытаний, использующих различные протоколы, для каждого исследуемого набора терапий и для каждого из типов рака. Эта задачу физически невозможно выполнить, более того, она связана с определенными этическими трудностями, так как результат взаимодействия препаратов вполне может и снизить общую эффективность терапии.

Стандартные и перспективные методы лечения онкологических заболеваний.
Существенную помощь в решении этой задачи может оказать относительно молодой подход в онкологии – математическое моделирование. Разумеется, оно ни в коем случае не может полностью заменить клинические исследования, но с помощью него можно существенно сузить круг потенциально эффективных схем лечения, требующих экспериментальной проверки. Исследованиями в этой области занимаются сотрудники Центра «Математическое моделирование в биомедицине» Максим Кузнецов и Андрей Колобов. Особое внимание они фокусируют на рассмотрении клинических схем, включающих антиангиогенную терапию, действие которой направлено на прекращение образования новых кровеносных сосудов, питающих опухоль. В теории такое воздействие должно приводить к ограничению притока питательных веществ к опухоли и замедлять ее рост.
Антиангиогенная терапия относится к классическим методам лечения, а именно – к группе таргетных терапий, цель которых – блокирование действия определенных «молекулярных мишеней», участвующих в росте опухоли. Вместе с этим она является довольно молодой и слабо изученной на практике терапией. Как правило, клинические испытания новых противоопухолевых препаратов сначала проводятся для опухолей высокой степени злокачественности – чтобы проверить лекарства в максимально трудных боевых условиях – и все антиангиогенные препараты оказались весьма малоэффективными для большинства таких опухолей. Но еще до осознания этого факта медицинским сообществом первый антиангиогенный препарат, авастин, получил клиническое одобрение для метастатически активной глиобластомы. И теперь в официальной информации по его назначению отмечено, что его применение в режиме монотерапии не увеличивает продолжительность жизни пациентов, позволяя на практике лишь несколько облегчить симптомы болезни. При этом последующие испытания анитиангиогенных препаратов продемонстрировали их значительную эффективность для доброкачественных опухолей. Такой же вывод относительно эффективности антиангиогенных препаратов для разных типов опухолей был независимо сделан нашими сотрудниками как раз с помощью математического моделирования.
Им удалось получить этот результат благодаря новому подходу к рассмотрению причин роста опухоли. В существующих математических моделях зачастую единственной причиной роста опухоли считается инвазия, т.е., прорастание раковых клеток в окружающую ткань. Этот тип роста характерен для опухолей высокой степени злокачественности. Потому такие опухоли сложно удалить хирургическим путем – оставшиеся клетки зачастую приводят к рецидиву болезни. Наши ученые, кроме этого, учитывают и другую причину – расталкивание окружающих тканей делящимися опухолевыми клетками. Этот тип роста имеет решающее значение для компактных доброкачественных опухолей. В процессе озлокачествления опухоли характер ее роста, как правило, изменяется с компактного на инвазивный, и рост реальной опухоли представляет собой комбинацию этих двух типов. Такой подход позволил нашим ученым мгновенно сделать выводы, на получение которых у медицинского сообщества ушло более десяти лет.
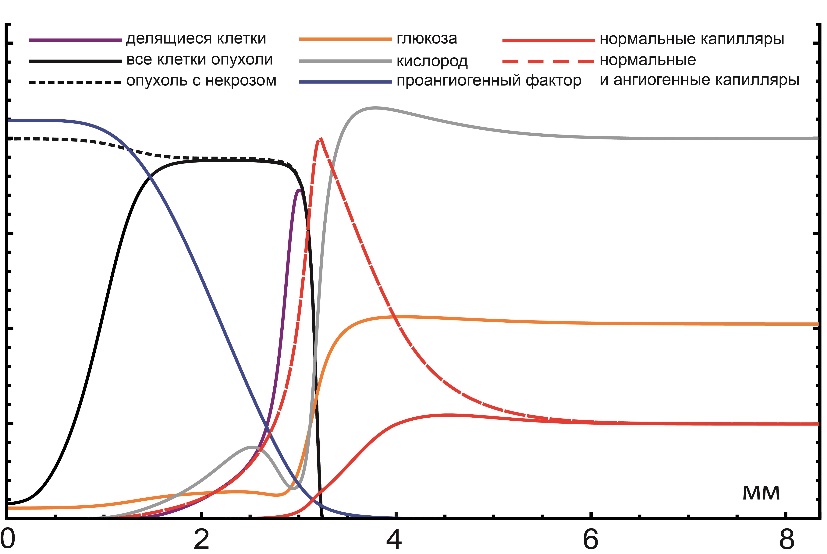
Пример распределения переменных в модели роста раковой опухоли
Теперь Максим и Андрей работают над моделированием комбинированного лечения, заключающегося в добавлении антиангиогенной терапии к химио- и радиотерапии. На практике такие методы лечения показывают неоднозначные результаты, так как разные виды противоопухолевой терапии взаимодействуют между собой довольно сложным образом: к примеру, антиангиогенная терапия может не только перекрыть поток питательных веществ к опухоли, но и снизить приток химиотерапевтического препарата. В целях наших ученых – определение ключевых факторов, влияющих на эффективность таких комбинированных лечений и предложение оптимальных клинических схем лечения. Тот факт, что модель уже доказала свою эффективность на деле, позволяет рассчитывать на значительные результаты и в этой задаче.
- Hits: 1956
Самоорганизация – проще, чем кажется
Явление самоорганизации определило все переходные моменты в истории нашего мира, начиная с самого рождения Вселенной: формирование первых атомов, звезд, планет, жизни, человеческого общества. Всеобщность этого явления делает его очень важным для научного исследования, однако необходимость междисциплинарного подхода препятствовала ему вплоть до середины прошлого века. Одной из первых работ в области самоорганизации стало исследование Алана Тьюринга, широко известного за свой вклад в математику, информатику и искусственный интеллект. В своей работе Алан Тьюринг предположил, что ключом к многим явлениям морфогенеза, то есть формирования органов у живых организмов, является неустойчивость пространственно-однородного состояния в системе диффундирующих по ткани и взаимодействующих друг с другом химических веществ, локальная концентрация которых влияет на поведение клеток, составляющих эту ткань. Такая неустойчивость может приводить к неоднородному распределению этих веществ и следовательно – к разному поведению клеток на разных участках ткани. По такому механизму, согласно гипотезе Тьюринга, у живых организмов на заданном расстоянии друг от друга могут образовываться щупальца, листья и другие органы. Кроме того, узоры на шкурах животных могут формироваться по аналогичному принципу. Поначалу гипотеза Тьюринга не принималась научным сообществом всерьез, но впоследствии она нашла широкое применение во множестве исследований не только биологических, но и физических, химических и даже социологических систем, в которых ключевыми процессами являются локальное взаимодействие элементов и их случайное передвижение в пространстве.

Структуры Тьюринга, впервые полученные в химическом эксперименте.
Алан Тьюринг вывел условия для образования стационарных структур в системах, состоящих из двух взаимодействующих элементов. Согласно им, один из элементов должен быть самоактиватором, увеличение концентрации которого стимулирует его собственное производство. Второй вид должен быть самоингибитором, действующим противоположным образом. Кроме того, подвижность – или коэффициент диффузии – самоингибитора должна быть достаточно выше, чем у самоактиватора – насколько именно, зависит от конкретных значений остальных параметров системы, которые определяют скорости реакций веществ и называются кинетическими. Эти условия составляют концепцию «короткодействующей активации и дальнодействующего ингибирования» (КАДИ). В дальнейшем эта концепция стала общепринятой и для систем с произвольным числом переменных. Основным ее недостатком является то, что, согласно ей, структуры Тьюринга могут возникать в значительном диапазоне кинетических параметров системы, только если подвижности переменных сильно различаются. При этом для химических и биологических систем это, как правило, не так – например, коэффициенты диффузии абсолютного большинства белков в животной ткани различаются не более, чем в несколько раз, что оставляет лишь узкое окно для значений кинетических параметров, при которых могут формироваться структуры. Эта черта является основным объектом критики теории Тьюринга – ведь в биологии, как правило, значения кинетических параметров варьируются в широких пределах как для разных особей, так и для разных участков ткани одной особи, а также просто со временем. Таким образом, с первого взгляда механизм, предложенный Тьюрингом, не является стабильным – то есть незначительное случайное изменение параметров модели запросто может привести к прекращению формирования структур – и в результате животное не получит необходимых ему органов или останется без узоров на шкуре.
Известным приемом, позволяющим значительно повысить стабильность механизма Тьюринга, является обратимое связывание вещества-самоактиватора с третьим, неподвижным, элементом, благодаря чему его эффективная подвижность может быть существенно замедлена. Благодаря этому методу структуры Тьюринга впервые были получены искусственно в 1990 году. Тем не менее, этот прием также вписывается в концепцию КАДИ. Однако в последние годы появились свидетельства того, что в многокомпонентных системах структуры Тьюринга могут формироваться и в обход общепринятой концепции. В частности, было продемонстрировано существование систем с одним неподвижным элементом, в которых структуры Тьюринга возникают при любых коэффициентах диффузии подвижных элементов. Сотрудники нашего Центра «Математическое моделирование в биомедицине» Максим Кузнецов и Андрей Полежаев занялись исследованием этого явления и впервые вывели общие условия, при которых системы обладают данным свойством.
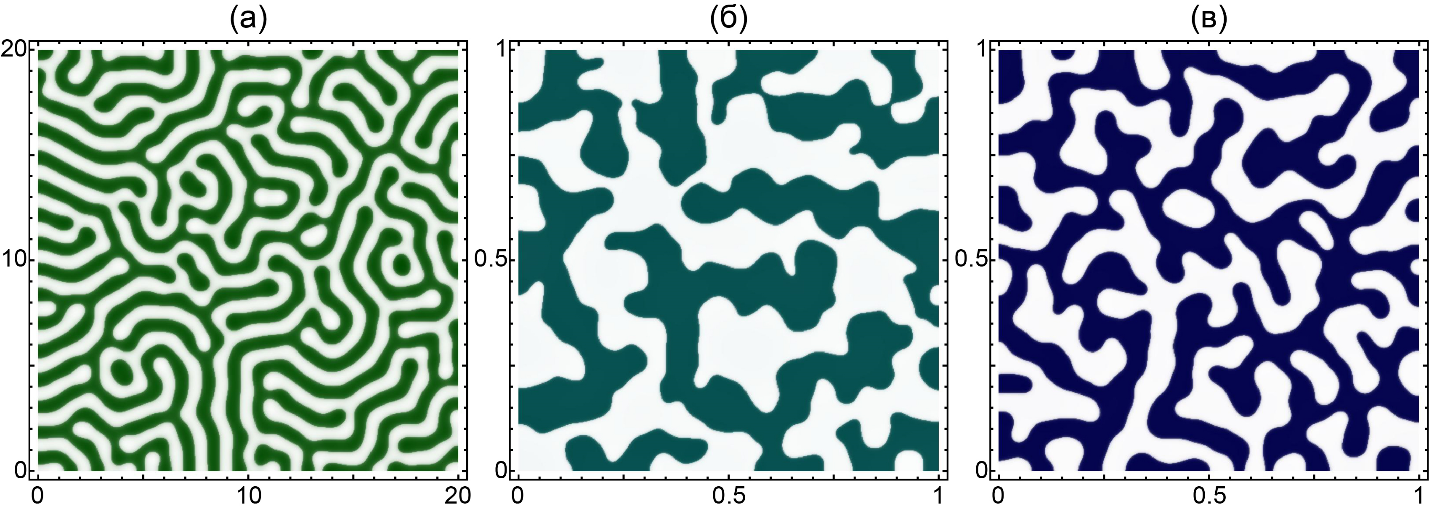
Структуры Тьюринга, возникающие при математическом моделировании трехкомпонентной системы с одним неподвижным элементом, при отношениях подвижностей двух других элементов: (а) 1; (б) 1000; (в) 0,001.
Оказалось, что при наличии в системе неподвижного элемента, не влияющего напрямую на собственное производство – то есть, не являющегося ни самоактиватором, ни самоингибитором – условия для формирования структур Тьюринга качественно изменяются. Особо любопытно, что при этом ключевую роль начинает играть схема типов взаимодействий этого элемента с двумя подвижными элементами. Под типом взаимодействия подразумевается один из трех случаев, в которых увеличение концентрации одного элемента: 1) стимулирует производство другого, 2) ингибирует его или 3) не влияет на него. Исследование, проведенное нашими сотрудниками, показало, что, при определенных схемах типах взаимодействий элементов в системе, структуры Тьюринга формируются в ней не только при любых коэффициентах диффузии подвижных элементов, но и при любых значениях кинетических параметров системы (по крайней мере, если в отсутствие диффузии система оказывается устойчива – иначе происходит борьба разных типов неустойчивостей, которая может приводить к разным результатам). Такие условия предлагают несколько более сложный, но гораздо более стабильный механизм формирования структур Тьюринга по сравнению с классическим – в то время как скорости реакций в биологии могут варьироваться в очень широких пределах, тип влияния одного элемента на другой обычно четко задан.
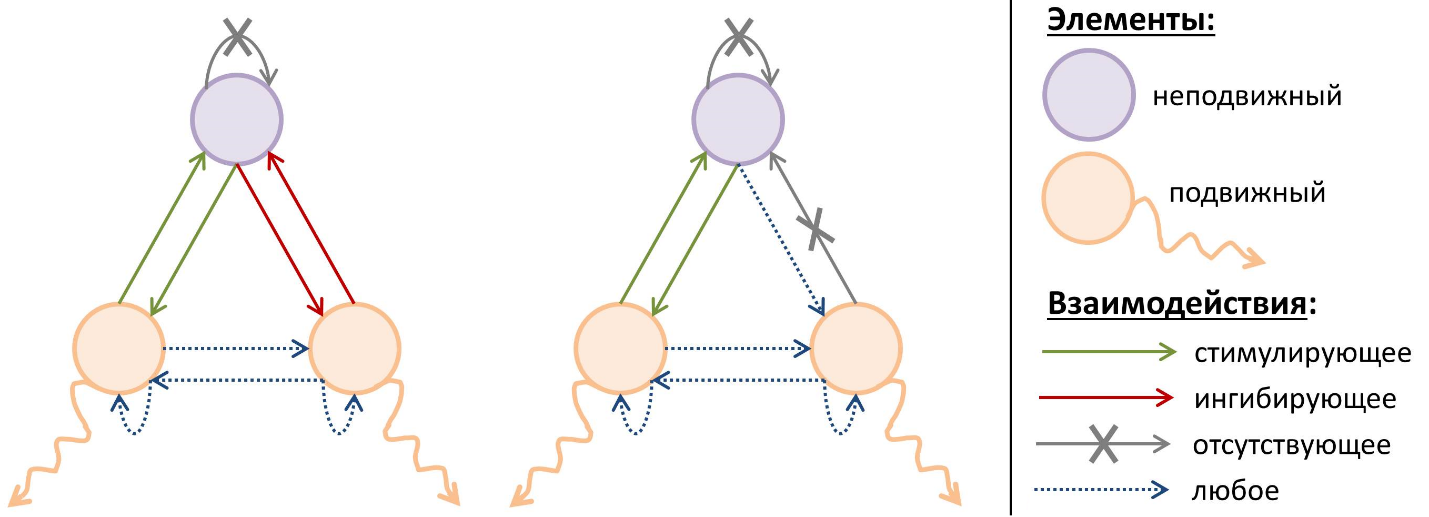
Примеры схем взаимодействий элементов, при которых неустойчивость Тьюринга проявляется при любых значениях параметров системы.
На данный момент неизвестно, реализуется ли такой механизм в живой природе, однако никакое из его условий не противоречит биологическим законам. Более того, так как развитие живого мира диктуется законами биологической эволюции, высокая стабильность найденного механизма должна обеспечить его распространение в природе при условии возможности его реализации. При этом необходимость наличия неподвижного элемента, взаимодействующего с подвижными, подчеркивает важность роли, которую в морфогенезе могут играть клеточные рецепторы, внутриклеточные сигнальные пути и другие элементы, связанные с неподвижными клетками, которые, как правило, игнорируются в математических моделях.
Подробнее об исследовании наших сотрудников можно будет прочесть в статье, на данный момент находящейся на этапе рецензирования в одном из ведущих физических журналов мира.
- Hits: 1703
Recordings: на Google Drive.
Recordings: on youtube
Recordings: on mathnet (english interface is available)
Other seminars and events of the Nikolskii Mathematical Institute
Connection link: click.
The seminar is under the lead of Prof. Vitaly Volpert
Secretary: Anastasiia Mozokhina, This email address is being protected from spambots. You need JavaScript enabled to view it.
Schedule (2024):
January 25 - Ivan Azarov
February 1 - Nikolai Bessonov (the talk will be in Russian)
February 8 - Jean Clairambault - Phenotype divergence and cooperation in isogenic multicellularity and in cancer
February 15 - Alberto d'Onofrio
February 22 - Ivan Azarov - Part 2
February 29 - Denis Pushin
March 28 - Mostafa Adimy
April 25 - Andjelka Hedrih
May 23 - Nikolay Pertsev - Stage-dependent models in immunology, application to the study of the development of HIV-1 infection
in the lymph node.
28.03.2024 [16:30 (MSK=UTC+3), online] Mostafa Adimy (INRIA) "Continuous-Time Differential-Difference Models in Population Dynamics and Epidemiology"
Abstract
Close
We are interested in models of population dynamics and epidemiology that involve two phases, one active and one inactive, with exchanges between the two phases. The durations of these two phases may be finite or infinite. Depending on the phenomenon under investigation, the active/inactive phases may have different interpretations. For example, in a population model composed of immature and mature individuals, the mature phase may be considered active and the immature phase inactive. In a predator-prey model, for example, the inactive phase may represent a refuge where the prey population is protected from predators. It may also represent a resting phase during which the predator does not hunt. In epidemiology, it may represent a period of immunity due to vaccination. For a population of cells, the inactive phase may correspond to the G1/G0 phase of the cell cycle, and the active phase to the stages S/G2/M leading to cell division. One of the questions addressed by this type of model is the impact of the inactive phase on the asymptotic behavior of the solutions in the system. We will use continuous-time differential-difference models to study these problems.
29.02.2024 [16:30 (MSK=UTC+3), online] Denis Pushin (National Medical Research Center for Hematology) "Mathematical modeling of shear-induced platelet activation in high shear flow"
Abstract
Close
Platelets feel shear stress in flowing blood via special sensors known as von Willebrand factor (VWF). These multimers undergo globule-stretch transition under high shear stress. When shear stress is larger than specific threshold VWF multimers unwind, exposing more domains capable of binding platelet receptors. Multivalent binding of VWF molecules with platelet receptors may lead to platelet activation and increasing of arterial thrombus formation risk.
The presentation will be dedicated to describing of mathematical approach for analyzing shear-induced platelet activation in large human vessels. It will be shown how the conditions of VWF unwinding under unsteady shear flows were established via combination of nonlinear dynamics and computational fluid dynamics methods. The application of the approach to analyzing of platelet activation in specific clinical settings will be given. In particular, it will be shown that “no activation” condition in large arteries obeys the power law relating the size of VWF multimers with blood volume flow rate through vessel.
22.02.2024 [13:00 (MSK=UTC+3), online] Ivan Azarov (M&S Decisions) "Reticular network as the Lymph Nodes railroad system: T-cells migration modeling by the free energy minimization technique" - Part 2
Abstract
Close
15.02.2024 [16:30 (MSK=UTC+3), online] Alberto d'Onofrio (University of Trieste) "Behavioral Epidemiology: the challenge if modeling the behavior of Policy makers"
Abstract
Close
In this talk I will review the main challenges of modeling the behavior if policymakers and it's impact on spread and control of infectious diseases.
08.02.2024 [16:30 (MSK=UTC+3), online] Jean Clairambault (Center Inria, Sorbonne University) "Phenotype divergence and cooperation in isogenic multicellularity and in cancer"
Abstract
Close
References:
1. Alvarez, F.E., Clairambault, J. Phenotype divergence and cooperation in isogenic multicellularity and in cancer (authors' preprint, June 2023), https://hal.science/hal-04145070. In revision, January 2024
2. Alvarez, F. E., Carrillo, J. A., Clairambault, J. Evolution of a structured cell population endowed with plasticity of traits under constraints on and between the traits. (authors' preprint), https://hal.science/hal-03344894. J Math Biol, 85:64, September 2022
01.02.2024 [16:30 (MSK=UTC+3), online] Nikolai Bessonov (Institute of Problems of Machine Science of the Russian Academy of Sciences) "The initial configuration is a new (or well–forgotten old) variable in mechanics; its application in problems of thermoelasticity, masselasticity, plasticity and others"
Abstract
Close
Video: (part2) https://www.youtube.com/watch?v=1f9W6JUFnRM
25.01.2024 [16:30 (MSK=UTC+3), online] Ivan Azarov (M&S Decisions) "Reticular network as the Lymph Nodes railroad system: T-cells migration modeling by the free energy minimization technique"
Abstract
Close
28.12.2023 [16:30 (MSK=UTC+3), online] Gustavo Zampier (Federal University of Rio Grande do Norte, School of Science and Technology) "How ephapticity communication can explain brain complexity?"
Abstract
Close
21.12.2023 [16:30 (MSK=UTC+3), online] Karam Allali (Hassan II University of Casablanca) "Optimal control of HPV infection and cervical cancer cells"
Abstract
Close
14.12.2023 [16:30 (MSK=UTC+3), online] Polina Kurbatova "Bioprocess modelling in vaccine production" - cancelled
Abstract
Close
07.12.2023 [16:30 (MSK=UTC+3), online] Malay Banerjee (IIT Kanpur) "Continuation of Turing pattern beyond the Turing domain"
Abstract
Close
However, such heterogeneous solutions depend on the stability of non-constant steady-states associated with the corresponding boundary value problem. This talk's main objective is to discuss the existence of stationary Turing patterns beyond the Turing instability domain and the detection of their bifurcations through the numerical continuation technique. The illustration will rely on a spatiotemporal prey-predator model with saturated cooperative hunting among the predators.
15.11.2023 [15:30 (MSK=UTC+3), online] Vitaly Volpert (Université Claude Bernard Lyon 1) "Mathematical modelling of respiratory viral infections" (joint with WMDS23)
Abstract
Close
26.10.2023 [16:30 (MSK=UTC+3), online] Léon Matar Tine (Université Claude Bernard Lyon 1) "Inflammation processes in Alzheimer disease modeling"
Abstract
Close
12.10.2023 [16:30 (MSK=UTC+3), online] Vitaly Volpert (RUDN) "Characterization of spatiotemporal dynamics in EEG data with optical flow patterns"
Abstract
Close
05.10.2023 [16:30 (MSK=UTC+3), online] Anass Bouchnita (University of Texas at El Paso) "Mathematical modeling of multiple myeloma intraclonal heterogeneity, drug resistance, and impact on erythropoiesis"
Abstract
Close
28.09.2023 [16:30 (MSK=UTC+3), online] Masoud Saade (RUDN) "Dynamics of Persistent Epidemic and Optimal Control of Vaccination"
Abstract
Close
21.09.2023 [16:30 (MSK=UTC+3), online] Vitaly Volpert (RUDN) "Mathematical modeling of EEG-dynamics"
Abstract
Close
08.06.2023 [16:30 (MSK=UTC+3), online] Dmitry Nechipurenko (Lomonosov Moscow State University) "Computational modeling of hemostatic response to various types of microvessel injuries"
Abstract
Close
01.06.2023 [16:30 (MSK=UTC+3), online] Alexander Bratus (Russian University of Transport) "Non-damped Nonlinear Wave in Continual Hypercycle Replicated Systems"
Abstract
Close
An important class of replicator models involves systems of nonlinear ordinary differential equations with dynamics restrained by the standard simplex in the state space and describes macromolecular interactions in various problems of population genetics and evolutionary game theory [1], as well as in theories of the origin of life [2]. Of special interest is the hypercycle model that was proposed by M. Eigen and P. Shuster classical hypercycle is a finite closed network of self-replicating macromolecules (species) which are connected so that each of them catalyzes the replication of the successor, with the last molecule reinforcing the first one. From the sociological perspective, the catalytic support for the replication of other molecules resembles altruistic behavior, in contrast to conventional autocatalysis. However, the actual number of macromolecules in a hypercycle may be huge, and this may significantly complicate the numerical analysis of the associated dynamical system. It may therefore be reasonable to represent the macromolecules as points in some line segment (of cardinality continuum) and to construct an appropriate distributed model of hypercyclic replication. Such a methodology was previously implemented for Crow–Kimura and Eigen quasispecies models, with a single integra-differential equation replacing a large number of ordinary differential equations [3,4]. Since the model represents an idealized process of replication continuous species in the form of integra-differential equation with space delay in integral simplex. The existence and uniqueness of positive solution are proved. The solutions represent sequence of non-damped nonlinear wave. It is proved existence of Andronov-Hopf bifurcation in steady state position [5]. The results of numerical modelling are presented.
[1] Hofbauer J., Sigmund К. Evolutionary Games and Population Dynamics. Cambridge University Press, 1998.
[2] Eigen M., Schuster P. The Hypercycle: A Principle of Natural Self-Organization. Springer-Verlag, Berlin Heidelberg New York, 1979.
[3] Bratus A.S., I. Yegorov, A. Novozhilov. Open quasispecies models: Stability, optimization, and distributed extension (печатный). Journal of Mathematical Analysis and Application, https://doi.org/10.1016/j.jmaa.2019.123477 2019.
[4] Братусь А.С., Дрожжин С. В., Якушкина Т. С. Математические модели эволюции и динамики репликаторных систем. Москва, УРСС, 2022, 265 с.
[5] Marsden J. E., McCracken M. The Hopf Bifurcation and its Applications. Springer, New York, 1976.
27.04.2023 [16:30 (MSK=UTC+3), online] Wissam El Hajj (Claude Bernard University Lyon 1) "Inflammation propagation modeled as a reaction-diffusion wave"
Abstract
Close
13.04.2023 [16:30 (MSK=UTC+3), online] Masoud Saade (RUDN) "An Epidemic Model with Time Delays Determined by the Infectivity and Disease Durations"
Abstract
Close
31.03.2023 [12:00 (MSK=UTC+3), online; Friday] Karam Allali (Hassan II University of Casablanca) "Global analysis of a time-delayed two-strain epidemic model with general incidence rates and therapy"
Abstract
Close
16.03.2023 [16:30 (MSK=UTC+3), online] Anass Bouchnita (The University of Texas at El Paso) "Continuous mathematical models of blood flow and their applications"
Abstract
Close
Simulating the movement of blood flow through the cardiovascular system has important applications in biomedicine such as improving our understanding of cardiovascular diseases, designing new therapeutics and medical devices, and planning surgical interventions. Several modelling approaches were developed to describe blood flow, ranging from continuous single-phase and multi-phase models, to particle-based methods such as the Lattice Boltzmann and the Dissipative Particle Dynamics methods. In this talk, we will discuss some of the continuous modelling methods that are commonly used to simulate blood flow. We begin by presenting the physiological and physical characteristics of blood flow in different conditions and locations of the cardiovascular system. Next, we introduce blood flow rheology models, including the ones that capture complex blood flow behavior such as shear thinning and discuss the effect of the hematocrit. Then, we present some multi-phase models of blood flow and discuss their derivation from the mixture theory and numerical implementation. We illustrate the advantage of the multi-phase models by showing their ability to model platelet margination and clot formation due to blood cell stagnation. After that, we discuss the challenges related to validation against experiments and the numerical implementation of these models.
02.03.2023 [16:30 (MSK=UTC+3), online] Yixiang Wu (Middle Tennessee State University) "Analysis of a Reaction-Diffusion Susceptible-Infected-Susceptible Epidemic Patch Model Incorporating Movement Inside and Among Patches"
Abstract
Close
I will talk about a reaction-diffusion susceptible-infected-susceptible (SIS) epidemic patch model. The individuals are assumed to reside in different patches, where they are able to move inside and among the patches. The movement of individuals inside the patches is descried by diffusion terms, and the movement pattern among patches is modeled by an essentially nonnegative matrix. We define a basic reproduction number $\mathcal{R}_0$ for the model and show that it is a threshold value for disease extinction versus persistence. The monotone dependence of $\mathcal{R}_0$ on the movement rates of infected individuals is proved when the dispersal pattern is symmetric or non-symmetric.
16.02.2023 [16:30 (MSK=UTC+3), online] D. V. Alekseev (Lomonosov MSU, HSE University), A. V. Galatenko (Lomonosov MSU, HSE University), V. V. Galatenko (Lomonosov MSU), S. A. Nersisyan (HSE University), V. M. Staroverov (Lomonosov MSU, HSE University) "Mathematical models of within-host COVID-19 dynamics"
Abstract
Close
Mathematical models of within-host COVID-19 dynamics are a convenient tool that allows estimating treatment efficiency, justifying isolation period as well as getting useful insights on underlying biological mechanisms. In our talk we first consider a number of analytical results on simple models consisting of two or three differential equations, and then present a more sophisticated model inspired by experiments on cell lines.
07.02.2023 [14:00 (MSK=UTC+3), online] Vitaly Volpert (RUDN), "Epidemic models with time delay" - postponed
Abstract
Close
In this lecture we will introduce a new class of epidemic models with distributed and point-wise delay. We will compare them with conventional compartmental models and will use them to describe the data on COVID-19 epidemic.
Joint Workshop with Analysis and Applied Mathematics https://sites.google.com/view/aam-seminars?pli=1
Connection link:
https://us02web.zoom.us/j/6678270445?pwd=SFNmQUIvT0tRaHlDaVYrN3l5bzJVQT09
Conference ID: 667 827 0445, Access code: 1
26.01.2023 [12:00 (MSK=UTC+3), online] Vitaly Volpert (RUDN), "Сomputational fluid dynamics and applications"
Abstract
Close
We will discuss plans for joint work of the polymer hydrodynamics modeling group and the Center for Mathematical Modeling in Biology and Medicine.
19.01.2023 [16:30 (MSK=UTC+3), online] Vitaly Volpert (RUDN), "Epidemic models based on daily infection rates"
Abstract
Close
In this lecture, we will introduce a new class of epidemic models based on the number of new infection cases. We will compare these models with conventional epidemiological models and will study their main properties.
22.12.2022 [16:30 (MSK=UTC+3), online] Ivan Kaspirovich (RUDN), "On some applications of Baumgarte's stabilization method"
Abstract
Close
Basically, the behavior of dynamical systems is described with the help of ordinary differential equations. Only for a few systems it is possible to find an analytical solution. Numerical integration methods are used to solve the majority of problems. However, when numerically integrating systems of motions equationsmotion with mechanical constraits, the effect of accumulation of rounding errors is possible with implementing a particular finite difference scheme. This can lead to instability of the numerical solution with respect to the constraint equations. To limit the magnitude of such accumulation J. Baumgarte proposed an algorithm to stabilize the constraints during numerical integration. The report is devoted to some applications of this method to modeling, optimization and inverse dynamical problems.
08.12.2022 [16:30 (MSK=UTC+3), online] Nader El Khatib (Lebanese American University), "Patient specific model of the Blood-Plaque-Wall interaction: an FSI mathematical model"
Abstract
Close
The inflammatory process of atherosclerosis leads to the formation of an atherosclerotic plaque inside the intima of the blood vessel. The plaque consists of a lipid core covered by a fibrous cap. This plaque narrows the lumen of the vessel it and interacts with the blood flow. This interaction may have dramatic consequences as the rupture of the plaque which leads possibly to a stroke or the formation of blood clots that also may lead to the obstruction of the blood vessel. This study is devoted to the FSI analysis of the interactions of the blood with the plaque and the vessel wall extended in the case of 3D realistic geometry of a carotid artery taken from MRI to analyze the flow and structures stresses.
24.11.2022 [16:30 (MSK=UTC+3), online] Aleksey Belyaev (Lomonosov Moscow State University), "Biomechanical features of the initial stages of platelet hemostasis"
Abstract
Close
Platelet adhesion and activation are essential initial processes of arterial and microvascular hemostasis, where high hydrodynamic forces from the bloodflow impede coagulation. The process relies on von Willebrand factor (VWF) - a linear multimeric protein of blood plasma plays a pivotal role in mechano-chemical regulation of shear-induced platelet aggregation (SIPA). Adhesive interactions between VWF and glycoprotein receptors GPIb are crucial for platelet recruitment under high shear stress in the near-wall layers of the fluid. This talk is focused on biomechanical aspects of primary platelet hemostasis and the implications of 3D computer simulations resolving the mechanics of individual blood cells and VWF multimers for numerical investigation of this process. Quantitative understanding of mechano-chemical processes involved in SIPA would potentially promote the discovery of new anti-platelet medication and the development of multi-scale numerical models of platelet thrombosis and hemostasis. This work was supported by the Russian Science Foundation ( № 22-21-00221, https://rscf.ru/en/project/22-21-00221/).
10.11.2022 [16:30 (MSK=UTC+3), online] Vitaly Volpert (Institut Camille Jordan, RUDN), "Do biological species exist as mathematical solutions?",
Abstract
Close
Joint meeting with Seminar on Analysis, Differential Equations and Mathematical Physics http://msrn.sfedu.ru/sl
According to Darwin, biological species can be characterized as groups of individuals with similar morphological characteristics. If we consider humans and take only one such characteristics, for example, their height, then the population can be described by the normal distribution. Such distributions considered for any biological species and their morphological parameters are relatively stable and can be considered as stationary in appropriate time scale. Therefore, we can formulate the question whether population distributions can be described as stable stationary solutions of some relevant models. However, it appears that conventional population models do not have such solutions. In this lecture, we will derive a model for a population distribution with respect to the genotype (and not phenotype, i.e., morphology). We will study the existence and stability of solutions of this equation, in particular, of normal distributions. We will conclude with some biological interpretations including the relation between the genotype and the phenotype. Joint work with B. Peña and S. Trofimchuk
Abstract: https://msrn-files.sfedu.ru/msrp/seminars_info/announcement_volpert.pdf
03.11.2022 [16:30 (MSK=UTC+3), online] Fedor Novikov (MolTech Ltd.), "Evaluation of Clinical PK & Toxicity of Antibody Drug Conjugate"
Abstract
Close
Antibody drug conjugates (ADCs) used in the treatment of cancer are designed to harness the specificity of targeted treatment and combine this with the potent cell-killing of a small molecule. ADCs have complex molecular structures, including the key components of a highly-selective monoclonal antibody (mAb) directed against a target of interest, a potent cytotoxic small molecule (payload), and a linker connecting these two species. This linker is intended to be stable in circulation and only release the payload once the ADC is internalized into cancerous target cells. This construct was designed to provide an improvement over the narrow therapeutic indices of cytotoxic small molecule drugs, theoretically resulting in an improved safety profile of the ADC when compared to systemic administration of the traditional chemotherapy agent.
For most ADCs currently in clinical development, doselimiting toxicities (DLTs) often appear to be off-target, in other words, independent of the target of the ADC. Since the small molecule payloads typically utilize a mechanism of action (MOA) of traditional anti-cancer chemotherapy agents, once the free payload is cleaved from the mAb, it can cause the same typical chemotherapy toxicities, including hematologic and non-hematologic AEs, such as peripheral neuropathy and hepatic toxicity. Many of these off-target AEs ultimately define the DLT of the agent, which in turn often dictates the maximum tolerated dose (MTD) and subsequently the dose used in pivotal studies and eventually clinical practice.
The analysis of PK and Toxicity data have been evaluated by statistical methods to combine and quantify the outcomes of a series of clinical trials in a single pooled analysis. The purpose of the analysis was to summarize the key clinical safety data published for ADCs by payload class, and data permitting, to establish a dose-response model for severe grade toxicity incidence as a function of payload, dose/regimen, and cancer type (solid tumor vs. hematologic cancer).
27.10.2022 [16:30 (MSK=UTC+3), online] Darya Apushkinskaya (RUDN University), "How free boundaries couple Salmonella with hysteresis"
Abstract
Close
20.10.2022 [16:30 (MSK=UTC+3), online] Tatiana Kovalenko (Center of Theoretical Problems of Physico-chemical Pharmacology), "Different modeling approaches in the simulation of extrinsic coagulation factor X activation: limitations and areas of applicability"
Abstract
Close
13.10.2022 [16:30 (MSK=UTC+3), online] Vitaly Volpert (Institut Camille Jordan, RUDN University), "Mathematical modeling of lung obstruction during respiratory viral infections"
Abstract
Close
Excessive mucus production and its increased viscosity due to respiratory viral infections can lead to its accumulation in the bronchi resulting in airway obstruction. We will discuss how to model mucus motion in normal and pathological conditions.
06.10.2022 [16:30 (MSK=UTC+3), online] Ghada Abi Younes (Claude Bernard University Lyon 1), "A Free Boundary Mathematical Model of Atherosclerosis"
Abstract
Close
Atherosclerosis is an inflammatory disease of the arterial wall that involves abnormal cholesterol deposits in the inner layers of arteries. The chronic accumulation of fat contributes to the formation of fibrofatty lesions, called atheromatous plaques, which grow through the opposite direction of the vessel and narrow the blood flow to vital organs.
In this work, we model the arterial inflammation in atherosclerosis in a one-dimensional free boundary problem. The plaque growth causing the motion of the domain boundary is not only considered as resulting from the influx of cells through the boundary, but also from their interaction in the subendothelial space. The main objective of this work is findinding the solution of the model and drawing conclusions on the plaque growth. For this purpose, we simplify the model, formulate the model, by a change of variables, with a fixed boundary, space and time dependent coefficients and non linear terms. The study of the latter model allows us to prove the existence of solution by applying the fixed point theorem. We also investigate the wave solution and analyze the numerical results. Finally, the results obtained are generalized to the original model.
22.09.2022 [16:30 (MSK=UTC+3), online] Anna Andreeva (Moscow Institute of Physics and Technology), "Analysis of point mathematical models of blood coagulation by numerical methods"
Abstract
Close
Mathematical modeling of blood coagulation is important for medical biophysics. We considered two mathematical models of the blood coagulation system (BCS). These models are ODE systems. The first model takes into account the role of activation reactions of blood coagulation factors on membranes and fibrin polymerization. The second model is reduced. The model describes a cascade of activation of blood coagulation factors, but does not take into account the process of fibrin polymerization. We used the one-step Rosenbrock’s method with complex coefficients (CROS) to solve the stiff ODE system. The method was realized on programming language C.
In our work, we considered the influence of factor XI and the release of factor V from platelets during their activation. Many parameters of mathematical models of blood coagulation are known with low accuracy (some of them - with an accuracy of several magnitude). Therefore, the task of analyzing the sensitivity of the BCS model to parameters occures. The analysis can be carried out in a variety of ways. 1) The system equations in variations is built and solved. Based on its solution, a dimensionless sensitivity function of concentrations to parameters was built. Based on this method, the sensitivity of the tenase complex to the numbers of sites and constants associated with the V factor were investigated. We tested the hypothesis that the composition of the lipid membrane has little effect on blood coagulation. A unified approach to the study of sensitivity by parameters and solving problems selection of the coefficients of the model on experimental data based on the solution of the system in variations was formulated. 2) We changed parameters one by one and monitor change in model calculations. The dependence of the lag period and endogenous thrombin potential on parameters, as well as on the initial concentrations of blood coagulation factors were investigated. The principal possibility of its research for the design of selective drugs is shown. There is a lack of factor VIII when a person has hemophilia A. Accordingly, the blood coagulates slowly or does not coagulates at all. A study of BCS for the post-infart state was carried out (at the same time, the concentration of factor XIa changes). Calculations are carried out at normal concentration of factor VIII and in case of its deficiency.
15.09.2022 [16:30 (MSK=UTC+3), online] Aleksey Lobanov (People's Friendship University of Russia, Institute of Control Sciences), "Task of localization primary signs of a brain stroke"
Abstract
Close
This report will tell about the way to solve the problem of localization of the primary signs of a brain stroke. The stages of data preprocessing, filtering, clustering are touched upon, methods for assessing damage are proposed. The task of finding the primary signs of stroke is important due to the subjectivity of visual analysis by a neurologist. As a result, when making decisions related to medical manipulations, an independent algorithmic assessment of the patient's condition is required. Usually, machine learning methods are used to solve such problems, but the specifics of the disease and its manifestations, as well as complex access to data, force us to think through approaches that bypass the use of machine learning in favor of more conservative methods.
16.06.2022 [16:30 (MSK=UTC+3), online] Fedor Novikov (MolTech Ltd.), "TSAR, a new graph–theoretical approach to computational modeling of protein side-chain flexibility: Modeling of ionization properties of proteins"
Abstract
Close
A new graph–theoretical approach called thermodynamic sampling of amino acid residues (TSAR) has been elaborated to explicitly account for the protein side chain flexibility in modeling conformation-dependent protein properties. In TSAR, a protein is viewed as a graph whose nodes correspond to structurally independent groups and whose edges connect the interacting groups. Each node has its set of states describing conformation and ionization of the group, and each edge is assigned an array of pairwise interaction potentials between the adjacent groups. By treating the obtained graph as a belief-network—a well established mathematical abstraction—the partition function of each node is found. In the current work we used TSAR to calculate partition functions of the ionized forms of protein residues. A simplified version of a semi-empirical molecular mechanical scoring function, borrowed from our Lead Finder docking software, was used for energy calculations. The accuracy of the resulting model was validated on a set of 486 experimentally determined pKa values of protein residues. The average correlation coefficient (R) between calculated and experimental pKa values was 0.80, ranging from 0.95 (for Tyr) to 0.61 (for Lys). It appeared that the hydrogen bond interactions and the exhaustiveness of side chain sampling made the most significant contribution to the accuracy of pKa calculations.
09.06.2022 [16:30 (MSK=UTC+3), online] Gerasim Krivovichev (Saint-Petersburg State University), "One-dimensional models of hemodynamics: comparison and analysis"
Abstract
Close
The report is devoted to the one-dimensional mathematical models of blood flow, obtained by the averaging of equations of hydrodynamics on the vessel cross-section. Some of the new models deal with the non-Newtonian property of blood and the dependence of the viscosity on hematocrit. The process of pulse wave propagation in model vascular systems is considered. During the numerical solution, the influence of the viscosity, non-Newtonian terms, the shape of the velocity profile, and hematocrit values on the obtained solutions is investigated.
02.06.2022 [16:30 (MSK=UTC+3), online] Tatiana Sharifullina (Lavrentyev Institute of Hydrodynamics), "Mathematical modeling and optimization of the embolization process of cerebral arteriovenous malformation"
Abstract
Close
Based on the materials of the Ph.D. dissertation, scientific supervisor: Alexander A. Cherevko
Cerebral arteriovenous malformation (AVM) is a disorderly tangle of degenerate fused blood vessels. One of the effective methods of treating AVM is embolization - filling pathological vessels with a special liquid hardening substance (embolic agent) in order to block blood flow through them. This method of surgical intervention is widely used, but still in some cases is accompanied by perioperative rupture of malformation vessels. The arteriovenous malformation embolization process is described as a process of joint filtration of two fluids inside the AVM: blood and embolic agent [1, 2]. To find optimal embolization scenarios, the task of optimal control is set. The target functionality and limitations are selected in accordance with medical indications, and the control is the embolic agent flow at the entrance to pathology. The influence of the amount of blood flow into the surrounding vascular system during embolization is studied [3]. There is a good coincidence of the calculated and clinical blood pressure when calculating the model with a given clinical blood flow [4, 5]. The solidification of the embolic agent between the stages of its supply by changing the cross-section of the AVM available for the flow of two liquid phases is taken into account [5]. In solving the problem, clinical data obtained during monitoring of hemodynamic parameters during neurosurgical embolization operations at the Academician E.N. Meshalkin National Medical Research Center.
Literature:
[1] Cherevko A. A. et al. Modeling of the optimal scenario of arteriovenous malformation embolization //Journal of Physics: Conference Series. – IOP Publishing, 2019. – Т. 1268. – №. 1. – С. 012017.
[2] Cherevko A. A. et al. Modelling of the arteriovenous malformation embolization optimal scenario //Royal Society open science. – 2020. – Т. 7. – №. 7. – С. 191992.
[3] Гологуш Т. С., Остапенко В. В., Черевко А. А. Математическое моделирование режима эмболизации артериовенозной мальформации с перетоками на основе модели двухфазной фильтрации //Журнал вычислительной математики и математической физики. – 2021. – Т. 61. – №. 9. – С. 1571-1584.
English version: Gologush T. S., Ostapenko V. V., Cherevko A. A. Mathematical modeling of embolization of arteriovenous malformations with overflows on the basis of the two-phase filtering //Computational Mathematics and Mathematical Physics. – 2021. – Т. 61. – №. 9. – С. 1546-1558.
[4] Черевко А. А., Гологуш Т. С., Остапенко В. В. Поиск оптимального решения задачи эмболизации артериовенозной мальформации методом роя частиц //Прикладная механика и техническая физика. – 2021. – Т. 62. – №. 4. – С. 9-21.
English version: Cherevko A. A., Gologush T. S., Ostapenko V. V. Search for AN Optimal Solution of the Problem of Arteriovenous Malformation Embolization by the Particle Swarm Method //Journal of Applied Mechanics and Technical Physics. – 2021. – Т. 62. – №. 4. – С. 530-541.
[5] Sharifullina T., Cherevko A., Ostapenko V. Optimal control problem arising in mathematical modeling of cerebral vascular pathology embolization //Scientific Reports. – 2022. – Т. 12. – №. 1. – С. 1-15.
26.05.2022 [16:30 (MSK=UTC+3), online] Sergei Petrovskii (University of Leicester), "Plankton-oxygen dynamics under the climate change: catastrophes, extinctions, and long transients"
Abstract
Close
The effect of climate change on population dynamics is widely recognised, usually with many adverse effects, often resulting in species extinctions and biodiversity loss. Population dynamics can also have feedback on the climate; however, this issue remains poorly understood. In my talk, I will focus on the effect that the global warming can have on plankton, in particular, on phytoplankton ability to produce oxygen. It is estimated that more than one half of the total atmospheric oxygen is produced in the oceans due to the photosynthetic activity of phytoplankton. Any significant decrease in the net oxygen production by phytoplankton is therefore likely to result in the depletion of atmospheric oxygen and in a mass mortality of animals and humans. However, the rate of oxygen production depends on water temperature and hence can be affected by the global warming. I address this issue theoretically by considering a novel model of a coupled plankton-oxygen dynamics where the rate of oxygen production changes with time to account for the ocean warming [1]. I first prove that the model, albeit being simple or “conceptual”, provides an upper bound for a class of complex realistic models of ocean (bio)dynamics [2,3]. I then show that, when the temperature rises sufficiently high, a regime shift happens: the sustainable oxygen production becomes impossible and the system’s dynamics leads to plankton extinction and oxygen depletion. I also consider a scenario when, after a certain period of increase, the temperature is set on a new higher yet apparently safe value, i.e. before the oxygen depletion disaster happens. I show that in this case the system dynamics may exhibit a long-term quasi-sustainable dynamics that can still result in the regime shift but only after a considerable delay: the phenomenon known as long transient dynamics [4,5]. Finally, I will argue that this catastrophe of the global oxygen depletion might have been the factor that resulted in a few mass extinctions in the Earth geological past.
[1] Sekerci Y, Petrovskii SV. (2015) Mathematical modelling of plankton-oxygen dynamics under the climate change. Bull. Math. Biol. 77, 2325-2353.
[2] Petrovskii SV, Sekerci Y, Venturino E. (2017) Regime shifts and ecological catastrophes in a model of plankton-oxygen dynamics under the climate change. J. Theor. Biol. 424, 91-109.
[3] Sekerci Y, Petrovskii SV. (2018) Global warming can lead to depletion of oxygen by disrupting phytoplankton photosynthesis: a mathematical modelling approach. Geosciences 8, 201.
[4] Hastings A, Abbott KC, Cuddington K, Francis T, Gellner G, Lai YC, Morozov A, Petrovskii SV, Scranton K, Zeeman ML. (2018) Transient phenomena in ecology. Science 361, eaat6412.
[5] Morozov A, Abbott KC, Cuddington K, Francis T, Gellner G, Hastings A, Lai YC, Petrovskii SV, Scranton K, Zeeman ML (2020) Long transients in ecology: Theory and applications. Physics of Life Reviews 32, 1-40.
05.05.2022 [16:30 (MSK=UTC+3), online] Benjamin Ambrosio (Le Havre Normandie University, The Hudson School of Mathematics), "Using reduced models to generate signals that resemble brain rhythms"
Abstract
Close
In this talk, I will discuss some models with the objective to generate signals that resemble brain rhythms. The requirement is to produce signals that have a main beat or frequency that we can somehow control but that are not periodic in the mathematical sense. We will discuss different aspects and confront with examples coming from neuroscience studies. This is joint work with Lai-Sang Young.
14.04.2022 [16:30 (MSK=UTC+3), online] Galina Valova (Lavrentyev Institute of Hydrodynamics), "Mathematical model of the brain hemolyquorodynamics in the application to the study of hydrocephalus"
Abstract
Close
There are a large number of pathological conditions of the central nervous system characterized by impaired movement of intracerebral fluids. An important example is hydrocephalus, a pathology in which the brain ventricles increase, which leads to displacement and compression of brain tissue. This condition is well described in terms of clinical manifestations, but its causes and development are poorly understood. The report considers a complex mathematical model of cerebral cerebrospinal fluid and hemodynamics of a person based on a model of multiphase poroelasticity for brain matter. The displacement of the ventricular wall of the brain and the magnitude of pressure on it are studied. Based on the MRI data of real patients, the patterns of behavior of these values are determined depending on the parameters of the model in hydrocephalus.
07.04.2022 [16:30 (MSK=UTC+3), online] Vitaly Volpert (Peoples’ Friendship University of Russia), "Virus mutation and competition in cell culture"
Abstract
Close
In the second lecture from the cycle of lectures devoted to mathematical modelling of viral infection and immune response, we will consider the case of two viruses in the same cell culture. They can be either independent or related by mutations. We will determine different regimes of infection spreading, its spreading speed and viral load.
24.03.2022 [16:30 (MSK=UTC+3), online] Ellina Grigorieva (Texas Woman’s University), "Optimal two- stage treatment protocol for a blood cancer model"
Abstract
Close
A two-stage combined treatment of blood cancer (leukemia, lymphoma) is considered for a given time interval. At the first stage, the patient is given a "hard" therapy (for example, chemotherapy) to achieve the normal functioning of the body; at the second stage, the patient is prescribed a "soft", maintenance therapy (for example, targeted therapy) to consolidate the achieved remission. The transition time from one therapy to another is not known in advance and depends on the patient's condition. Such treatment is mathematically described by a two-dimensional controlled Lotka-Volterra competition model, the variables of which are the concentrations of healthy and cancerous cells, and two bounded control functions reflect the applied methods of treatment. For such a controlled model, the aim is to minimize the objective function, which is the sum of the total weighted difference in the concentrations of cancer and healthy cells over the entire treatment interval, as well as these weighted differences taken both at the time of changing the therapy used and at the end of the treatment protocol. It is assumed that the moment of changing the type of therapy is not predetermined; it is found as a result of solving the stated minimization problem. Optimal solutions are obtained numerically using the BOCOP-2.0.5 environment and then discussed in detail. Conclusions are drawn about the effectiveness of two-stage combined treatment and the possibility of finding the optimal treatment protocol for a real cancer patient.
10.03.2022 [16:30 (MSK=UTC+3), online] Vitaly Volpert (Peoples’ Friendship University of Russia), "Mathematical immunology and epidemiology of respiratory viral infections"
Abstract
Close
This series of lectures will present the issues of mathematical modeling of respiratory viral infections. In the first lecture, the question of the spread of a viral infection in cell culture will be considered.
24.02.2022 [16:30 (MSK=UTC+3), online] Ghada Abi Younes (Claude Bernard Lyon 1 University in France), "Mathematical Modeling of the Interaction of Inflammation and Chemotaxis in Atherosclerosis: Formation of Fatty Streaks"
Abstract
Close
Atherosclerosis is a chronic in ammatory disease that develops progressively through continuous evolution of arterial wall lesions. It is characterized by the accumulation of lipids inside the arterial wall resulting in inflammatory responses. We study the early stages of atherosclerosis with a mathematical model based on reaction-diffusion equations. The model includes the main factors in atherosclerosis and focuses on the positive feedback between the inflammation in atherosclerosis and the chemotactic movement of macrophages. Stability analysis and numerical simulations for a reduced model including macrophages and inflammatory cytokines show the formation of spatial structures corresponding to the emergence of fatty streaks as a result of interaction between chemotaxis and inflammation. Finally, we consider the complete model taking into account also endothelial cells and growth factor that provides a more realistic description of the disease and extend the results obtained by performing numerical simulations.
10.02.2022 [Общий семинар, 16:30, online] Anass Bouchnita (University of Texas at Austin), "A new class of COVID-19 compartmental models that explicitly incorporates the changes in population-immunity"
Abstract
Close
The COVID-19 landscape has been rapidly changing during the last few months. Several new effects have been influencing COVID-19 transmissibility and severity such as waning immunity, vaccination, emerging variants of concern. As a result, mathematical models that describe COVID-19 transmission dynamics are becoming very complex, highly-dimensional and computationally expensive. In this talk, we will introduce a new class of COVID-19 epidemiological models that explicitly describe the changes in the population-immunity and their effects on COVID-19 transmissibility and severity. We begin by presenting the derivation of the model from a more complex multiscale immuno-epidemiological model. Then, we discuss how this new class of models allows the integration of vaccination and immune waning in a simple and meaningful way, by applying it to determine the optimal timing for switching from primary vaccination of the younger population to giving additional doses to high risk groups. Finally, we show how this new modeling technique was used to accurately estimate the impact of Omicron emergence in the US.
References:
1. Bouchnita, Anass, et al. "COVID-19 Scenario Projections: The Emergence of Omicron in the US-January 2022." (2022).
27.01.2022 [Общий семинар, 16:30, online] Veronika Voronova (M&S Decisions), "Optimization of immunooncology drug discovery using mathematical modeling"
Abstract
Close
Immunotherapies are one of the most promising strategies for cancer treatment as they enable achieving stable remission in patients with advance cancer stages. High variability in treatment response is one of the key problems in oncopharmacology in general and in oncoimmunology in particular. Combinations of medicines and personalization of the therapy can be used to gain maximal treatment efficacy and mathematical modeling serves as a tool for optimization of these strategies. The presentation will be focused on application of mathematical model, characterizing immune response, in development of combination immunotherapies.
Смотреть запись (video): https://www.youtube.com/watch?v=D1EA1xgLE2Y
13.01.2022 [Общий семинар, 16:30, online] Косинский Юрий Анзельмович, "Математическое моделирование механизмов приобретенной резистентности B-клеточных лимфом к ингибиторам BTK" / Yuri Kosinsky "Mathematical modeling helps to better understand the mechanisms B-cell lymphomas acquired resistance to BTK inhibitor treatment"
Abstract
Close
Тирозин киназа Брутона (BTK) опосредует передачу сигнала от B-клеточных рецепторов к внутриклеточным сигнальным путям, что признано одним из ключевых механизмов в патогенезе B-клеточных лимфом. Идея использование ингибитора BTK ибрутиниба для лечения B-клеточных лимфом выглядела перспективной, однако в клинических испытаниях была показана низкая эффективность препарата из-за подавляющей доли пациентов с первичной резистентностью или быстрым проявлением приобретенной резистентности.
Резистентность B-клеточных лимфом к ибрутинибу может быть обусловлена как генетическими мутациями, так и негенетическими механизмами адаптации – например, активацией альтернативных сигнальных путей, ответственных за выживание лимфомных клеток и которые не зависят от ингибирования BTK. В работе мы моделировали механизмы регуляции активности сигнальных путей и транскрипции генов, которые обеспечивают переключение лимфомной клетки в резистентный фенотип под воздействием ингибитора BTK.
Chronic activation of B-cell receptor (BCR) signaling via Bruton tyrosine kinase (BTK) is largely considered to be one of the primary mechanisms driving disease progression in B-cell lymphomas, particularly, ABC DLBCL. Although the BTK-targeting agent ibrutinib has shown promising clinical responses, the presence of primary or acquired resistance is common that leads to disease progression. Resistance to ibrutinib therapy can be mediated through genetic mutations, up-regulation of alternative survival pathways, or other unknown factors that are not targeted by ibrutinib therapy. In this work we did mathematical modeling of signaling pathways and transcriptional perturbations in B-cell lymphoma cells under BTK inhibitor treatment which might leads to ibrutinib resistant phenotype.
Смотреть запись (video): https://www.youtube.com/watch?v=9ka7WTZKMj0
30.12.2021 [Общий семинар, 16:30, online] Кристина Леон, "Моделирование врожденного и адаптивного иммунного ответа на вирусную инфекцию типа SARS" / Cristina Leon "Modelling of the innate and adaptive immune responses to SARS viral infection"
Abstract
Close
В данной работе мы разрабатываем модель иммунного ответа на вирусную инфекцию с учетом некоторых особенностей вируса SARS-CoV-2. На первом этапе мы изучаем врожденный иммунный ответ, основанный на защитных свойствах интерферона, секретируемого инфицированными вирусом клетками. После этого мы вводим адаптивный иммунный ответ с антигенспецифическими Т- и В-лимфоцитами. Предлагаемая модель была откалибрована, объединив существующие математические модели с экспериментальными и клиническими данными об инфекциях SARS-CoV и SARS-CoV-2. Модель предсказывает корреляцию между максимальной и начальной вирусной нагрузкой при заражении. Кроме того, мы показываем, что инкубационный период зависит от начальной вирусной нагрузки и индивидуального иммунного ответа. Далее мы изучаем возникновение цитокинового шторма из-за чрезмерной выработки провоспалительных цитокинов. Таким образом, исследование обеспечивает лучшее понимание и прогнозирование взаимодействия между респираторными вирусными инфекциями и иммунным ответом.
In this work, we develop an ODE model of the immune response to viral infection taking into account some particular properties of the SARS-CoV-2 virus. At the first stage, we study the innate immune response based on the protective properties of interferon secreted by virus-infected cells. After that, we introduce the adaptive immune response with antigen-specific T and B lymphocytes. The proposed model was calibrated combining the existing mathematical models with the experimental and clinical data on SARS-CoV and SARS-CoV-2 infections.
The model predicts the correlation between the maximal and the initial viral loads upon infection. Additionally, we show that incubation period depends on the initial viral load and individual immune response. Next, we study the emergence of cytokine storm due to the excessive production of proinflammatory cytokines. Thus study provides a better understanding and predicting the interaction between respiratory viral infections and the immune response.
Смотреть запись (video): https://www.youtube.com/watch?v=di4UWVqSlt0
23.12.2021 [Общий семинар, 16:30, online] Вольперт Виталий Айзикович "Математическое моделирование теплового взрыва"
Abstract
Close
В этой обзорной лекции мы познакомимся с основами теории теплового взрыва, начиная с классических работ Семенова и Франк-Каменецкого, а также рассмотрим некоторые более современные результаты по взаимодействию теплового взрыва с конвекцией.
Смотреть запись (video): https://www.youtube.com/watch?v=jMat0qzjdQM
16.12.2021 [Общий семинар, 16:30, online] Леоненко Василий Николаевич "Прогнозирование эпидемий ОРВИ в городах России с учетом структуры населения и уровня иммунитета" / Vasiliy Leonenko "Forecasting epidemics of acute respiratory infections in Russian cities considering the population structure and the immunity levels"
Abstract
Close
Доклад будет посвящен методикам прогнозирования динамики эпидемических ОРВИ в России на примере гриппа и COVID-19 с помощью компартментальных и мультиагентных моделей, а также анализу связи между формированием иммунитета и последующими волнами заболеваемости острыми респираторными инфекциями.
The talk will address short-term forecasting of severe ARI dynamics in Russia via compartmental and multiagent models, with influenza and COVID-19 as case studies, and the connection between the immunity formation and the consequent incidence waves of severe acute respiratory infections.
Смотреть запись (video): https://www.youtube.com/watch?v=RO0fo8rCeDQ
09.12.2021 [Общий семинар, 14:00, online] Vitaly Volpert "Theory and applications of reaction-diffusion waves".
Abstract
Close
The theory of reaction-diffusion waves and its applications will be considered in the talk.
02.12.2021 [Общий семинар, 16:30, online] Jochen Mau "An axiomatic approach to human-body functional biodynamics".
Abstract
Close
The axiomatic theory kernel for further translation into models of specific complex-systems dynamics in health and medicine rests upon a separation of functional organization from material realization, and casts dynamic features of physiological function into mathematical equations from a phenomenological perspective. Multi-scale complexity is resolved in a hierarchical drill-down from coarse to fine, finer and finer decomposition of functional aggregates, starting with person's whole body. Extensions to social interaction become possible when a person's behaviour expresses interaction of body's major functional components. Different from ``parts models'' under a modular modelling paradigm, specifications of parts can always be integrated into the holistic set-up. As a practical advantage, empirical investigations can start at the macro level of whole body, and gradually proceed down to lower level functional components, in a kind of “functional peeling”.
Смотреть запись (video): https://www.youtube.com/watch?v=VTgsqfjCSsY
18.11.2021 [Общий семинар, 16:30, online] Vitaly Volpert "Waves and pulses for monotone reaction-diffusion systems".
Abstract
Close
This lecture will begin with some known results about reaction-diffusion waves followed by some new results about stationary pulses. Investigation of the existence of such solutions is based on the theory of elliptic problems in unbounded domains, while the analysis of their stability uses some spectral properties. The applications of these results will be illustrated for various biological and biomedical models.
Смотреть запись (video): https://www.youtube.com/watch?v=1wAiiwTrAOg&t=3433s
21.10.2021 [Общий семинар, 16:30, online] Елена Михальченко "Моделирование камеры сгорания двигателя с вращающейся детонационной волной" / Elena Mikhalchenko "Modeling of a rotating detonation engine combustion chamber"
Abstract
Close
В работе рассмотрено трехмерное численное моделирование камеры сгорания двигателя с непрерывной детонационной волной с помощью авторского программного пакета. Программное обеспечение использует математическую модель для многокомпонентного химически реактивного газа, опционально используя модель турбулентности. В основе модели химической кинетики лежит механизм элементарных реакций, в зависимости от механизма меняется число реакций. В программе, в том числе, реализован авторский кинетический механизм. Рассмотрено шесть кинетических механизмов: механизм Мааса – Варнаца – Поупа, механизм Hong, механизм Вильямса, механизм Gri-Mech 3.0, механизм Ли – Джоу –Казаков – Драер и авторский кинетический механизм, проведено их сравнение. Код распараллелен с помощью технологий OpenMP и MPI. В результате работы программы была получена оптимальная форма камеры сгорания с самоподдерживающейся детонационной волной на смеси водород-воздух.
A 3D numerical modeling of a rotation detonation engine combustion chamber was modeled using authors’ software. The software uses a mathematical model for multicomponent chemically reacting gas with turbulence, optionally. The chemical kinetics uses elementary reactions; their number depends on the choice of mechanism. An authors’ chemical mechanism is among other six. The kinetic mechanisms are as follows: Maas, Warnatz, Pope; Hong; Williams; Gri-Mech 3.0; Lie, Zhao, Kazakov, Dryer; and authors’ kinetic mechanism. The results for those mechanisms are compared. The code is parallelized using OpenMP and MPI techniques. An optimal shape of the self sustaining rotating detonation engine combustion chamber using a hydrogen-oxygen mixture was obtained.
Смотреть запись (video): https://www.youtube.com/watch?v=FpbTK1ejLGk&t=1s
07.10.2021 [Общий семинар, 16:30, online] Jean Clairambault "Plasticity in cancer cells and emergence of drug resistance: what consequences for therapeutics?".
Abstract
Close
Drug-induced drug resistance, the question I am tackling from a theoretical point of view, maybe due to biological mechanisms of different natures, local regulation, epigenetic modifications (reversible) or genetic mutations (irreversible), according to the extent to which the genome of the cells in the cell population is affected. The modelling framework of adaptive dynamics I will present corresponds biologically to epigenetic modifications.
I will address an optimal control problem in the context of two populations, healthy and cancer, both endowed with phenotypes evolving with drug pressure, and competing for space and nutrients in a non-local Lotka-Volterra-like way, taking into account a double constraint of limiting unwanted adverse effects and avoiding the emergence of drug resistance.
Time permitting, I will conclude by proposing a list of open challenging questions to modellers and mathematicians about the emergence and evolution of cancer itself.
Ссылка на презентацию: читать
Смотреть запись (video): https://www.youtube.com/watch?v=4bulBIpgFyI
23.09.2021 [Общий семинар, 16:30, online] Malay Banerjee "Stability and bifurcation in interacting population models with slow-fast time scale".
Abstract
Close
Stable coexistence is an important terminology in the context of interacting population models. Ordinary differential equation models of interacting populations admit two types of stable coexistence: steady-state and oscillatory. Large amplitude stable coexistence and global bifurcation of such attractors sometimes lead to extinction of one or more species. Recently, researchers are interested in understanding the large amplitude oscillation in interacting population models in the presence of a slow-fast time scale. In this talk, I will explain in detail the various kinds of oscillatory dynamics observed in interacting population models with slow-fast time scales along with the relevant terminology - canard oscillation and relaxation oscillation.
Ссылка на презентацию: читать
Смотреть запись (video): https://www.youtube.com/watch?v=0NSsO3IFfBY&t=484s
09.09.2021 [Общий семинар, 16:30, online] Карандашев Я.М. "Моделирование динамики горения водорода при помощи полносвязной нейронной сети UNET". / Iakov Karandashev "Simulation of hydrogen combustion dynamics using a fully connected UNET neural network"
Abstract
Close
Расчет физико-химических взаимодействий газодинамических процессов, проходящих в двигателях, является трудоемкой задачей. Если рассчитывается нестационарный процесс, включающий такие физические явления, как детонация, зажигание горючей смеси, распространение волн горения, то получение расчетных данных даже за весьма малое физическое время требует долгой работы суперкомпьютерных систем. Попытка же ускорить время расчета обычными для этого простыми методами, такими как огрубление расчетной сетки или экстраполяция результатов, полученных на начальном этапе расчета, на значительно больший временной период, не гарантирует отсутствия грубых отклонений численной от исходной математической модели. В настоящей работе рассматривается задача горения водорода с кислородом в присутствии нейтральных элементов (азот (N2) и аргон (Ar)). В процессе горения образуются различные водородно-кислородные соединения (H2, O2, H2O, OH, HO2, H2O2, H, O), меняется температура смеси. Такой процесс преобразования веществ описывается 28 уравнениями химических реакций (механизм GriMech 3.0 (1999)). В итоге требуется проследить развитие данной системы от некоторого начального состояния на несколько шагов по времени. В настоящей работе показано, что нейросетевая архитектура UNET может быть успешно применена к задаче предсказания детерминированных многомерных временных рядов, а именно моделирования химических процессов горения, описываемых жёсткой системой обыкновенных дифференциальных уравнений. Используя её, нам удалось обучить компактную модель, которая может аппроксимировать изменения концентраций веществ в смеси в процессе химических реакций с высокой степенью точности, достаточной чтобы рекуррентно получать предсказание на сотни и даже тысячи шагов интегрирования вперёд, занимая при этом на порядок меньше времени вычисления, чем численное интегрирование. Данная работа является развитием идей, описанных в работе [1]. Изменив нормировку данных и немного архитектуру сети (см. рисунок), удалось не только улучшить точность и надежность нейронной сети, но и уменьшить вычислительные затраты.
Calculation of physicochemical interactions of gas-dynamic processes taking place in engines is a laborious task. If a non-stationary process is calculated, including such physical phenomena as detonation, ignition of a combustible mixture, propagation of combustion waves, then obtaining calculated data even for a very short physical time requires a long operation of supercomputer systems. An attempt to speed up the calculation time using the usual simple methods, such as coarsening of the computational grid or extrapolation of the results obtained at the initial stage of the calculation for a much longer time period, does not guarantee the absence of gross deviations of the numerical from the original mathematical model. In this work, we consider the problem of combustion of hydrogen with oxygen in the presence of neutral elements (nitrogen (N2) and argon (Ar)). During combustion, various hydrogen-oxygen compounds are formed (H2, O2, H2O, OH, HO2, H2O2, H, O), the temperature of the mixture changes. This process of transformation of substances is described by 28 equations of chemical reactions (mechanism GriMech 3.0 (1999)). As a result, it is required to trace the development of this system from some initial state by several steps in time. This paper shows that the UNET architecture neural network can be successfully applied to the problem of predicting deterministic multidimensional time series, namely, modeling the chemical combustion processes described by a rigid system of ordinary differential equations. Using it, we were able to train a compact model that can approximate changes in the concentrations of substances in a mixture during chemical reactions with a high degree of accuracy, sufficient to recursively obtain predictions for hundreds and even thousands of integration steps forward, while taking an order of magnitude less computation time than numerical integration. This work is a development of the ideas described in work [1]. By changing the data normalization and the network architecture (see figure), we managed not only to improve the accuracy and reliability of the neural network, but also to reduce computational costs.
Презентация (pptx): читать
Смотреть запись (video): https://www.youtube.com/watch?v=KhuIoD126jA&t=711s
01.07.2021 [Общий семинар, 16:30, online] Беляев А.В. "Механо-чувствительные белки крови и их роль в клеточном гемостазе" / Aleksey Belyaev "Mechano-sensitive blood proteins and their role in cellular hemostasis"
Abstract
Close
Гемостаз – это сложная системная реакция крови на повреждение или воспаление эндотелия сосудов. Этот процесс состоит из нескольких этапов, из которых можно выделить два основных явления: агрегацию тромбоцитов и свертывание плазмы крови. Многие белки участвуют в инициации, регуляции и ингибировании этих процессов, например обеспечивающий каскад реакций полимеризации фибрина, агрегации и активации тромбоцитов, химической сигнализации и распространения автоволн свертывания. Первичный клеточный гемостаз в артериях, артериолах и венулах основан на агрегации тромбоцитов в месте повреждения. Поскольку обычно этот процесс инициируется в условиях интенсивного кровотока, гидродинамические силы оказывают существенное влияние на рост и структуру тромбоцитарного агрегата. По современным представлениям, ключевую роль на первом этапе агрегации тромбоцитов играют механо-чувствительные белки, присутствующие как в плазме крови, так и на мембранах тромбоцитов.
Конформационные изменения, происходящие в этих белках под действием гидродинамических и механических сил, приводят к изменению из биохимической активности, что в результате может сказаться на росте тромба. Различные нарушения этой механо-химической регуляции приводят к таким синдромам, как тромботическая тромбоцитопеническая пурпура, кровоточивость или, напротив, избыточное тромбообразование. В данном докладе рассматриваются некоторые методы компьютерного моделирования белков в гидродинамическом потоке вязкой жидкости как инструмент для предсказательного моделирования нарушений системы клеточного гемостаза и решения связанных практических задач. Работа выполнена при поддержке РФФИ (19-01-00480 , 19-31-70002).
Hemostasis is a complex systemic reaction of the blood to damage or inflammation of the vascular endothelium. This process consists of several stages, from which two main phenomena can be distinguished: platelet aggregation and blood plasma coagulation. Many proteins are involved in the initiation, regulation, and inhibition of these processes, for example, they accelerate fibrin polymerization, platelet aggregation and activation, chemical signaling, and the propagation of coagulation autowaves. Primary cellular hemostasis in arteries, arterioles and venules is based on platelet aggregation at the site of injury. Usually, this process is triggered under conditions of intense blood flow, hydrodynamic forces have a significant effect on the growth and growth of the platelet aggregate. According to modern concepts, mechanosensitive proteins present both in blood plasma and on platelet membranes play a key role at the first stage of platelet aggregation. Conformational changes occurring in these proteins under the influence of hydrodynamic and mechanical forces cause a change in biochemical activities, which can affect the growth of a thrombus. Various disorders of this mechanochemical regulation cause a syndrome such as thrombotic thrombocytopenic purpura, bleeding or, on the contrary, excessive thrombosis. In this case, some methods of computer modeling of mechanisms in a hydrodynamic flow of a viscous fluid as a tool for predicting violations of the cellular hemostasis system and solving related practical problems. This work was supported by the Russian Foundation for Basic Research (19-01-00480, 19-31-70002).
03.06.2021 [Общий семинар, 16:30, online] Cristóbal Bertoglio. "MRI-based modeling of blood flows".
Abstract
Close
Mathematical and computational modeling of the cardiovascular system is increasingly giving alternatives to traditional invasive clinical procedures, and allowing for richer diagnostic metrics. In blood flows, the personalization of the models relies on inverse problems using clinical data, in particular medical images for measuring both anatomy and function of the vasculature. In this talk I will review methods to integrate models and data in the context of blood flows.
20.05.2021 [Общий семинар, 16:30, online] Бердников С.В. "Опасные природные явления на Юге России: события, наблюдения и перспективные задачи. Часть 2" / Sergey Berdnikov "Natural hazards in the South of Russia: events, observations, and perspective tasks. Part 2"
Abstract
Close
В период 2007-2014 гг. на юге России произошел ряд событий, связанных с опасными природными явлениями, которые нанесли значительный ущерб:
- 11 ноября 2007 г. в результате сильного шторма в Керченском проливе (между Черным и Азовскими морями) затонуло более 14 судов, один танкер разломился пополам, в акваторию вылилось более 2000 тонн мазута;
- 25-28 октября 2009 г. из-за сильного «цветения» воды была прекращена подача питьевой воды жителям г. Волгодонск на берегу Цимлянского водохранилища (р. Дон);
- 12 июля 2012 г. экстремальный дождевой паводок на р. Адагум (Западный Кавказ, левый приток р. Кубань) привел к затоплению г. Крымск, кроме материального ущерба имелись и человеческие жертвы;
- 23 марта 2013 г. и 24 сентября 2014 г. дельта р. Дон была затоплена в результате экстремальных штормовых нагонов, ущерб для жителей в каждом случае превысил 500 млн. руб.
В докладе дается краткая информация:
- о Южном научном центре РАН, сотрудники которого были непосредственными свидетелями этих событий, проводили исследования на месте;
- о каждом из рассмотренных выше событиях;
- подходах к мониторингу, прогнозированию, оценке рисков;
- задачи, требующие решения.
In the period 2007-2014, a number of events related to natural hazards, which caused significant damage, occurred in the South of Russia:
— On November 11, 2007, as a result of a strong storm in the Kerch Strait (between the Black and Azov Seas), more than 14 ships sank, one tanker broke in half, over 2000 tons of fuel oil spilled into the water;
— On October 25–28, 2009, due to a strong "blooming" of water in the Tsimlyansk reservoir (the Don River), the supply of drinking water to Volgodonsk was stopped;
— On July 12, 2012 extreme flash flood on the Adagum River (Western Caucasus, left tributary of the Kuban River) led to the flooding of the Krymsk, in addition to material damage, there were also human casualties;
— two extreme storm surges on March 23, 2013 and September 24, 2014 led to the flooding the delta of the Don River, the damage to residents in each case exceeded 500 million rubles.
The presentation provides brief information:
— about the Southern Scientific Center of the Russian Academy of Sciences, whose employees were direct witnesses of these events, conducted research on the spot;
— about each of the listed events;
— approaches to monitoring, hazards forecasting and risk assessment;
— tasks to be solved.
Презентация (pdf), часть 1: читать
Презентация (pdf), часть 2: читать
13.05.2021 [Аспирантский семинар, 16:30, online] Безяев В.И. "О некоторых методах алгебры и анализа в математической биологии. Часть II" / Vladimir Bezyaev "On some methods of algebra and analysis in mathematical biology. Part II"
Abstract
Close
Ссылка для подключения (connection link): подключиться к трансляции.
06.05.2021 [Институтский семинар, 16:30, online] Чернявский И.Л. "Особенности кровообращения и процессов переноса в плаценте человека. Часть 2 (доклад на английском языке)" / Igor Chernyavsky "A Story of Two Circulations: Blood Flow and Transport in the Human Placenta. Part 2"
Abstract
Close
Плацента человека — уникальный многофункциональный орган, который не только поддерживает развитие плода, но и определяет здоровье человека на протяжении всей жизни. Обмен веществ в плаценте происходит в виллезных деревьях, которые содержат сеть извилистых капилляров и взаимодействуют с кровью матери, текущей в неоднородной пористой среде. Несмотря на то, что процессы переноса на микро-масштабах описываются известными моделями, соответствующие усредненные модели и их статистические свойства на уровне тканей и органов гораздо менее изучены [1]. В данном докладе, представлен краткий обзор прогресса в математическом моделировании функции плаценты человека на основе данных трехмерной микроскопии и микро-томографии [2]. Моделирование демонстрирует неожиданную роль микроструктуры в усредненном описании процессов переноса. Также получены упрощенные модели, которые обладают определенной универсальностью [3]. Предложенные подходы могут найти применение для моделирования обмена веществ и в других сложных микро-сосудистых системах.
The human placenta is a unique multi-functional organ. It is a life-support system that not only nourishes a growing fetus, but also determines his or her life-long health. The placental primary exchange units, terminal villi, host complex networks of fetal capillaries and are interfaced with maternal blood, percolating a disordered porous medium. While placental transport at the micro-scale can be described by established models, systematically upscaling the transport and quantifying the associated uncertainty at the organ-level remain open challenges [1]. This talk will summarise recent progress in advanced 3D microscopy and its assimilation into mathematical models that predict placental function [2]. The models reveal a surprising role of microstructure in the upscaled predictions and demonstrate certain universality of reduced-order approximations for a wide class of solutes [3]. The developed approaches could also be useful for quantifying solute exchange in other complex microvascular systems.
Список литературы / References
1. Jensen O.E. & Chernyavsky I.L. (2019) Annu Rev Fluid Mech 51:25 (doi.org/10.1146/annurev-fluid-010518-040219).
2. Tun W.M., et al. (2020) bioRxiv 2020.12.07.411462 (doi.org/10.1101/2020.12.07.411462).
3. Erlich A., et al. (2019) Sci Adv 5:eaav6326 (doi.org/10.1126/sciadv.aav6326).
Скачать презентацию: pdf.
22.04.2021 [Общий семинар, 16:30, online] James E. Moore Jr. "Biotransport Mechanisms in Adaptive Immunity".
Abstract
Close
Lymph nodes are immune information collection and transfer junctions, where immune cells are housed in sufficient numbers and varieties to develop effective immune responses. It is therefore the job of the lymphatic system to gather information, including free antigen, antigen presenting cells, cytokines and other immune cells/signals, from the periphery and deliver them to the node for further processing. This requires an exquisitely complex combination of active pumping, cell/antigen transport, and biological signaling between multiple cell types. Once inside the node, the information must be relayed to the correct region, where carefully orchestrated processes in specific nodal compartments result in the production of antigen-reactive cells and/or antibodies. These processes also rely on fluid flow and cytokine transport. Understanding immune system transport processes provides opportunities to modulate immune function. Employing a combination of in vivo and excised vessel experiments, along with multiscale lumped parameter modeling, we have analyzed the effects of local pressure conditions and vasoactive substances on vessel pumping dynamics. We have also performed a series of experiments and computational simulations of flow patterns through and within lymph nodes. We have included the 3D distribution of blood vessels within lymph nodes due to the presence of significant transmural fluid movement. Agent-based models have been developed to explore the role of lymph node swelling in T cell population dynamics. Pumping dynamics of afferent vessels, and therefore the delivery of immune information to lymph nodes, are strongly affected by variations in local pressure, including the external pressure and vasoactive effects of vaccinations. Within lymph nodes, lymph flow provides guiding cues for antigen presenting cells to interact with B and T cells. Lymph node swelling facilitates the expansion of specific T cell populations. A better understanding of these transport phenomena could lead to more relevant criteria for designing methods to modulate the immune system effectively for health benefit, including vaccines.
Скачать презентацию: pdf.
15.04.2021 [Аспирантский семинар, 16:30, online] Безяев В.И. "О некоторых методах алгебры и анализа в математической биологии" / Vladimir Bezyaev "On some methods of algebra and analysis in mathematical biology"
Abstract
Close
Ссылка для подключения (connection link): подключиться к трансляции.
08.04.2021 [Общий семинар, 16:30, online] Бердников С.В. "Опасные природные явления на Юге России: события, наблюдения и перспективные задачи" / Sergey Berdnikov "Natural hazards in the South of Russia: events, observations, and perspective tasks"
Abstract
Close
В период 2007-2014 гг. на юге России произошел ряд событий, связанных с опасными природными явлениями, которые нанесли значительный ущерб:
- 11 ноября 2007 г. в результате сильного шторма в Керченском проливе (между Черным и Азовскими морями) затонуло более 14 судов, один танкер разломился пополам, в акваторию вылилось более 2000 тонн мазута;
- 25-28 октября 2009 г. из-за сильного «цветения» воды была прекращена подача питьевой воды жителям г. Волгодонск на берегу Цимлянского водохранилища (р. Дон);
- 12 июля 2012 г. экстремальный дождевой паводок на р. Адагум (Западный Кавказ, левый приток р. Кубань) привел к затоплению г. Крымск, кроме материального ущерба имелись и человеческие жертвы;
- 23 марта 2013 г. и 24 сентября 2014 г. дельта р. Дон была затоплена в результате экстремальных штормовых нагонов, ущерб для жителей в каждом случае превысил 500 млн. руб.
В докладе дается краткая информация:
- о Южном научном центре РАН, сотрудники которого были непосредственными свидетелями этих событий, проводили исследования на месте;
- о каждом из рассмотренных выше событиях;
- подходах к мониторингу, прогнозированию, оценке рисков;
- задачи, требующие решения.
In the period 2007-2014, a number of events related to natural hazards, which caused significant damage, occurred in the South of Russia:
— On November 11, 2007, as a result of a strong storm in the Kerch Strait (between the Black and Azov Seas), more than 14 ships sank, one tanker broke in half, over 2000 tons of fuel oil spilled into the water;
— On October 25–28, 2009, due to a strong "blooming" of water in the Tsimlyansk reservoir (the Don River), the supply of drinking water to Volgodonsk was stopped;
— On July 12, 2012 extreme flash flood on the Adagum River (Western Caucasus, left tributary of the Kuban River) led to the flooding of the Krymsk, in addition to material damage, there were also human casualties;
— two extreme storm surges on March 23, 2013 and September 24, 2014 led to the flooding the delta of the Don River, the damage to residents in each case exceeded 500 million rubles.
The presentation provides brief information:
— about the Southern Scientific Center of the Russian Academy of Sciences, whose employees were direct witnesses of these events, conducted research on the spot;
— about each of the listed events;
— approaches to monitoring, hazards forecasting and risk assessment;
— tasks to be solved.
25.03.2021 [Общий семинар, 16:30, online] Тютюнов Ю.В. "Пространственная модель трофической системы диатомовые микроводоросли – гарпактикоидные копеподы" / Yuri Tyuityunov "Spatial model of trophic system diatomic microalgae – harpacticoid copepods"
Abstract
Close
Построена и исследована модель, объясняющая мелкомасштабную пятнистость в трофической системе бентосные диатомовые микроводоросли – гарпактикоидные копеподы. Модель — система трёх дифференциальных уравнений с частными производными с краевыми условиями нулевого потока на границах прямоугольной области. Перемещения плотности копепод описаны классическим выражением потока Пэтлака — Келлер — Сегеля, включающим таксис и диффузию. Использована гипотеза опосредованного трофотаксиса, стимулируемого сытостью потребителя. Поскольку воспроизводство и смертность копепод являются медленными процессами, они игнорируются в модели, что, в силу граничных условий, обеспечивает постоянство средней плотности популяции потребителя. Анализ модели показал, что пространственно-неоднородные режимы невозможны при неспособности потребителя к пищевым миграциям. Вычисления с параметрами, идентифицированными на базе полевых наблюдений, воспроизводят хаотическую динамику с характерными размерами и временем жизни пятен плотности моделируемых видов. При этом, и плотность микроводорослей, и рацион копепод превышают значения, достигаемые в системе без трофотаксиса. Таким образом, продемонстрирована эволюционная устойчивость моделируемого пищевого поведения гарпактикоидных рачков.
A model capable of explaining small-scale spatial heterogeneity in trophic system consisting of diatom microalgae and benthic copepod crustaceans (order Harpacticoida) was built and investigated. The model is a system of three partial differential equations of the taxis–diffusion–reaction type. The Neumann boundary condition specifies zero-flux through the borders of a rectangular habitat. The movements of copepods are described by the classical Patlak — Keller — Segel flux expression, which includes both taxis and diffusion. The feeding migrations of consumers are modelled as indirect prey–taxis stimulated by harpacticoid satiety. Inasmuch as demographic processes in the predator population occur at slow time scale, the model includes no birth/death terms for predator. Hence, taking into account the boundary condition, the average density of predators remains constant. The analytical condition for the oscillatory instability of the homogeneous stationary state of species coexistence reveals the crucial role of the indirect prey–taxis for emergence of spatiotemporal patterns in the system. With parameters identified based on field observation data, the model simulates small-scale spatial patterns with characteristic size and the expected lifetime of density patches typical for the considered community of benthic organisms. In spatially heterogeneous dynamics both density of microalgae and individual consumption of harpacticoid copepods exceed equilibrium values observed without feeding migrations. This suggests that prey–taxis behaviour of the consumer is an evolutionary advantageous strategy.
11.03.2021 [Общий семинар, 16:30, online] Чернявский И.Л. "Особенности кровообращения и процессов переноса в плаценте человека" / Igor Chernyavsky "A Story of Two Circulations: Blood Flow and Transport in the Human Placenta"
Abstract
Close
Аннотация. Плацента человека — уникальный многофункциональный орган, который не только поддерживает развитие плода, но и определяет здоровье человека на протяжении всей жизни. Обмен веществ в плаценте происходит в виллезных деревьях, которые содержат сеть извилистых капилляров и взаимодействуют с кровью матери, текущей в неоднородной пористой среде. Несмотря на то, что процессы переноса на микро-масштабах описываются известными моделями, соответствующие усредненные модели и их статистические свойства на уровне тканей и органов гораздо менее изучены [1]. В данном докладе, представлен краткий обзор прогресса в математическом моделировании функции плаценты человека на основе данных трехмерной микроскопии и микро-томографии [2]. Моделирование демонстрирует неожиданную роль микроструктуры в усредненном описании процессов переноса. Также получены упрощенные модели, которые обладают определенной универсальностью [3]. Предложенные подходы могут найти применение для моделирования обмена веществ и в других сложных микро-сосудистых системах.
The human placenta is a unique multi-functional organ. It is a life-support system that not only nourishes a growing fetus, but also determines his or her life-long health. The placental primary exchange units, terminal villi, host complex networks of fetal capillaries and are interfaced with maternal blood, percolating a disordered porous medium. While placental transport at the micro-scale can be described by established models, systematically upscaling the transport and quantifying the associated uncertainty at the organ-level remain open challenges [1]. This talk will summarise recent progress in advanced 3D microscopy and its assimilation into mathematical models that predict placental function [2]. The models reveal a surprising role of microstructure in the upscaled predictions and demonstrate certain universality of reduced-order approximations for a wide class of solutes [3]. The developed approaches could also be useful for quantifying solute exchange in other complex microvascular systems.
Список литературы / References
1. Jensen O.E. & Chernyavsky I.L. (2019) Annu Rev Fluid Mech 51:25 (doi.org/10.1146/annurev-fluid-010518-040219).
2. Tun W.M., et al. (2020) bioRxiv 2020.12.07.411462 (doi.org/10.1101/2020.12.07.411462).
3. Erlich A., et al. (2019) Sci Adv 5:eaav6326 (doi.org/10.1126/sciadv.aav6326).
Скачать презентацию: pdf.
04.03.2021 [Аспирантский семинар, 16:30, online] Неверова Д.А. "Нелокальное реакционно-диффузионное уравнение с бистабильной нелинейностью" / Daria Neverova "Nonlocal reaction-diffusion equation with bistable nonlinearity. II part"
Abstract
Close
Ссылка для подключения (connection link): подключиться к трансляции.
25.02.2021 [Общий семинар, 15:00, online] Шаварова Е.К. "Methods for measuring blood pressure used in cardiology" / Elena Shavarova ""
Abstract
Close
В докладе планируется осветить особенности существующих методов измерения артериального давления (АД), применяемых в кардиологии, а также обозначить используемые математические алгоритмы для расчета параметров центральной гемодинамики и предполагаемые перспективы научных исследований в этой области.
The report will highlight the features of existing methods for measuring arterial blood pressure used in cardiology, the mathematical algorithms used to calculate the parameters of central hemodynamics, and the prospects for scientific research in this area.
Презентация: скачать.
18.02.2021 [Аспирантский семинар, 16:30, online] Куценко И.Л., Дюрягин О.В. "Моделирование базы данных на основе представленных данных больных гипертонией" / Irina Kutsenko, Oleg Dyuryagin "Database modeling based on the presented data of patients with hypertension"
Abstract
Close
Ссылка для подключения (connection link): подключиться к трансляции.
11.02.2021 [Институтский семинар, 16:30, online] Purnedu Mishra. "The role of indirect prey‐taxis and interference among predators in pattern formation".
Abstract
Close
We discuss a simple model describing a consumer/predator which, besides random dispersion, searches for food by moving toward the gradient of some chemical released by prey. The predator's rate of consumption is assumed to drop due to interference among predators when too many of them encounter on some aggregate of prey. The latter is assumed to have negligible motility with its density governed by an ODE. The interference among consumers is modeled by a modification of the Beddington's de Angelis functional response. Detailed numerical simulations of an auxiliary system indicate that nonconstant steady states imitating patches of species occur in the model provided taxis strength is big enough.
Презентация: скачать.
04.02.2021 [Аспирантский семинар, 16:30, online] Неверова Д.А. "Нелокальное реакционно-диффузионное уравнение с бистабильной нелинейностью" / Daria Neverova "Nonlocal reaction-diffusion equation with bistable nonlinearity"
Abstract
Close
Ссылка для подключения (connection link): подключиться к трансляции.
28.01.2021 [Аспирантский семинар, 16:30, online] В.А. Вольперт. "Взаимодействие миграции населения и распределения богатства" / Vitaly Volpert "Interaction of population migration and wealth distribution"
Abstract
Close
На динамику человеческих популяций могут влиять различные социально-экономические факторы, через показатели как рождаемость и смертность, а также интенсивность и направления миграции. В данной работе мы изучаем экономико-демографическую модель, которая учитывает зависимость скорости производства материальных ценностей от имеющихся ресурсов. В случае нелокального потребления ресурсов однородное в пространстве распределение богатства и населения заменяется периодическим в пространстве распределением, при котором общее богатство увеличивается. Для глобального потребления ресурсов, если перераспределение богатства достаточно мало, то однородное распределение заменяется гетерогенным с одним центром накопления богатства. Таким образом, экономические и демографические характеристики нелокальной и глобальной экономик могут сильно отличаться по сравнению с местной экономикой.
14.01.2021 [Общий семинар, 16:30, online] Ю.В. Василевский. "Математические модели в областях, близких к реальной анатомии. Часть 2" / Yuri Vassilevski "Mathematical modeling for real human anatomy. Part 2"
Abstract
Close
Математическое моделирование физиологических процессов в областях, близких к реальной анатомии, остается сложной задачей. Реалистичные расчетные геометрии, отражающие анатомическую структуру, важны как для пациент-ориентированных моделей, так и для фантомных моделей. Многие биомедицинские приложения основаны на персонализированной трехмерной реконструкции частей тела или всего тела человека, представленных медицинскими изображениями. Для таких приложений важными являются как уравнения модели и методы их приближенного решения, так и расчетные области и сетки. В докладе мы рассмотрим методологию построения персонализированных математических моделей для нескольких медицинских приложений: моделирование электроимпедансной диагностики, моделирование ультразвуковой диагностики, оценка гемодинамической значимости стенозов коронарных артерий, моделирование кровотока в левом желудочке сердца, моделирование закрытия реконструированного аортального клапана. Доклад представляет результаты, полученные в группе, состоящей из исследователей ИВМ РАН, МФТИ, Сеченовского Университета.
Mathematical modeling of physiological processes in domains close to real human anatomy remains a challenge. Realistic geometry that reflects an anatomical structure is important for both patient-oriented models and phantom models. Many biomedical applications are based on personalized 3D reconstruction of parts of the human body or the entire body represented by medical images. For such applications, the model equations and methods of their approximate solution, computational domains and grids are equally important. In the lecture, we will consider a methodology for building personalized mathematical models for several medical applications: modeling of electrical impedance diagnostics, modeling of ultrasound diagnostics, assessment of the hemodynamic significance of coronary artery stenosis, modeling blood flow in the left ventricle of the heart, modeling the closure of the reconstructed aortic valve. We present results obtained in a group consisting of researchers from the INM RAS, MIPT, and Sechenov University.
Презентация: скачать.
17.12.2020 [Общий семинар, 15:30, online] Ю.В. Василевский. "Математические модели в областях, близких к реальной анатомии" / Yuri Vassilevski "Mathematical modeling for real human anatomy. Part 2"
Abstract
Close
Математическое моделирование физиологических процессов в областях, близких к реальной анатомии, остается сложной задачей. Реалистичные расчетные геометрии, отражающие анатомическую структуру, важны как для пациент-ориентированных моделей, так и для фантомных моделей. Многие биомедицинские приложения основаны на персонализированной трехмерной реконструкции частей тела или всего тела человека, представленных медицинскими изображениями. Для таких приложений важными являются как уравнения модели и методы их приближенного решения, так и расчетные области и сетки. В докладе мы рассмотрим методологию построения персонализированных математических моделей для нескольких медицинских приложений: моделирование электроимпедансной диагностики, моделирование ультразвуковой диагностики, оценка гемодинамической значимости стенозов коронарных артерий, моделирование кровотока в левом желудочке сердца, моделирование закрытия реконструированного аортального клапана. Доклад представляет результаты, полученные в группе, состоящей из исследователей ИВМ РАН, МФТИ, Сеченовского Университета.
Mathematical modeling of physiological processes in domains close to real human anatomy remains a challenge. Realistic geometry that reflects an anatomical structure is important for both patient-oriented models and phantom models. Many biomedical applications are based on personalized 3D reconstruction of parts of the human body or the entire body represented by medical images. For such applications, the model equations and methods of their approximate solution, computational domains and grids are equally important. In the lecture, we will consider a methodology for building personalized mathematical models for several medical applications: modeling of electrical impedance diagnostics, modeling of ultrasound diagnostics, assessment of the hemodynamic significance of coronary artery stenosis, modeling blood flow in the left ventricle of the heart, modeling the closure of the reconstructed aortic valve. We present results obtained in a group consisting of researchers from the INM RAS, MIPT, and Sechenov University.
References:
1. Yu.Vassilevski, M.Olshanskii, S.Simakov, A.Kolobov, A.Danilov. Personalized Computational Hemodynamics. Models, Methods, and Applications for Vascular Surgery and Antitumor Therapy. Academic Press, 2020
2. A.Danilov, S.Rudnev, Yu.Vassilevski. Numerical Basics of Bioimpedance Measurements. In: Bioimpedance in Biomedical Applications and Research (eds. F.Simini and P.Bertemes-Filho), Springer International Publishing, 2018, p.117-135.
3. K.Beklemysheva, A.Danilov et al. Transcranial ultrasound of cerebral vessels in silico: proof of concept. Russ. J. Numer. Anal. Math. Modelling. 2016, V.31, No.5, p.317-328.
4. J.Carson, S.Pant, et al. Non‐invasive coronary CT angiography‐derived fractional flow reserve (FFR): A benchmark study comparing the diagnostic performance of four different computational methodologies. Int J Numer Meth Biomed Engng. 2019;e3235.
5. A.Danilov, A.Lozovskiy et al. A finite element method for the Navier-Stokes equations in moving domain with application to hemodynamics of the left ventricle. Russ. J. Numer. Anal. Math. Modelling,. 2017, V.32, No.4, p.225-236.
6. V.Salamatova, A.Liogky et al. Numerical assessment of coaptation for auto-pericardium based aortic valve cusps. Russ. J. Numer. Anal. Math. Modelling 34(5):277-287, 2019
7. A.Danilov, A.Yurova. Automated segmentation of abdominal organs from contrast-enhanced computed tomography using analysis of texture features. Int. J.Num.Meth. Biomed. Engng., 36(4) e3309
03.12.2020 [Аспирантский семинар, 15:00, online] М.К. Леон. "Математическая модель появления, конкуренции и сосуществования штаммов вирусов в зависимости от генотипа вируса" / Cristina Leon "Mathematical model of the emergence, competition and coexistence of virus strains depending on the virus genotype"
Abstract
Close
Данная работа посвящена изучению математической модели, которая рассматривает процессы, влияющие на концентрацию вируса u(x, t), с учетом мутации вируса, его репродукции и зависящей от генотипа смертности, как естественной, так и определяемой антивирусным лечением. После определения условий для появления штаммов вирусов изучается сосуществование вирусов, добавляя второе уравнение вируса v(y, t).
Распределение плотности вирусов u(x, t) и v(y, t) рассматривается как функции генотипов x и y, непрерывные как по генотипу, так и по времени t. Уравнения полученной модели образуют систему уравнений реакции-диффузии с интегральными членами, характеризующими конкуренцию вируса за клетки-хозяева.
Ссылка для подключения (connection link): подключиться к трансляции.
19.11.2020 [Аспирантский семинар, 15:00, online] А.А. Токарев. "Качественный анализ дифференциальных уравнений. Линейные системы на плоскости".
Abstract
Close
Ссылка для подключения (connection link): подключиться к трансляции.
19.11.2020 [Аспирантский семинар, 15:00, online] Ф.А. Сёмин. "Эффективное описание электромеханического сопряжения в модели миокарда".
Abstract
Close
Ссылка для подключения (connection link): подключиться к трансляции.
22.10.2020 [Общий семинар, 16:30, online] Т.М. Гамилов. "Использование синтетических баз данных для подбора параметров моделей гемодинамики".
Abstract
Close
На данный момент существует большое количество моделей кровотока, позволяющих прогнозировать воздействие различных сосудистых патологий на гемодинамические параметры. Одной из проблем внедрения этих моделей в клиническую практику является их способность подстраиваться под определённого пациента. Для настройки модели требуется определённый набор данных, измерить которые напрямую обычно невозможно или крайне затратно. Для подбора этих параметров предлагается использовать синтетическую базу данных. Эта база данных сгенерирована с помощью квазиодномерной модели кровотока и включает в себя 4374 виртуальных пациента. Подбор нужных параметров обеспечивается за счет обученной нейронной сети, обеспечивающей связь между легкодоступными (возраст, ЧСС, артериальное давление и т. д.) и труднодоступными параметрами (скорость пульсовой волны в аорте).
Ссылка для подключения (connection link): подключиться к трансляции.
Презентация: скачать.
15.10.2020 [Общий семинар, 16:30, online] Р.М. Третьякова. "Фильтрация жидкости в однородной среде со смешанным граничным условием".
Abstract
Close
Рассматривается трехмерная задача фильтрации вязкой жидкости в области, содержащей однородную пористую среду. Фильтрация описывается законом Дарси-Бринкмана. Граница среды разделена на три части: с условием непротекания, с условием на поток вектора скорости, или с условием на давление. Методом теории потенциала строится интегральное представление для скорости и давления жидкости. Формулируется система интегральных уравнений, удовлетворяющая граничным условиям. Уравнения решаются численно методом кусочно-постоянных аппроксимаций и коллокаций. Численная схема тестируется на задачах с разными граничными условиями. Исследуется также влияние вязкости на течение. Тестирование демонстрирует высокую точность численного метода.
Ссылка для подключения (connection link): подключиться к трансляции.
01.10.2020 [Общий семинар, 16:30, online] В.Н. Гурьянова. "Современные методы классификации одноканальных электрокардиограмм", часть 2.
Abstract
Close
На текущий момент существуют мобильные устройства, которые могут считывать одноканальную ЭКГ в домашних условиях. Эти устройства могут быть использованы для предварительного скрининга различных заболеваний. В данном докладе будет рассказано о различных методах, которые позволяют классифицировать одноканальные мобильные ЭКГ с достаточно высоким качеством. Многие из этих методов и улучшений к ним были предложены впервые автором доклада. В докладе выделены достоинства и недостатки предложенных методов. Стоит отметить, что все рассмотренные методы могут быть обобщены для работы с традиционными ЭКГ.
Ссылка для подключения (connection link): подключиться к трансляции.
Презентация: скачать.
24.09.2020 [Общий семинар, 16:30, online] М.Б. Кузнецов. "Детерминированный хаос".
Abstract
Close
Одним из самых значительных научных открытий последних десятилетий является открытие детерминированного хаоса в динамических системах. Суть этого открытия состоит в том, что полностью детерминированная динамическая система при отсутствии любых случайных воздействий на неё может вести себя непредсказуемым образом. Но у этой непредсказуемости при более внимательном рассмотрении удается найти ряд закономерностей в поведении системы, что отличает данное явление от классических случайных процессов. Подобные режимы наблюдаются в очень многих динамических системах, которые рассматриваются в математике, физике, химии, биологии, медицине, экономике и других областях.
Ссылка для подключения (connection link): подключиться к трансляции.
Презентация: скачать.
[ПЕРЕНЕСЁН НА 01.10.2020] 17.09.2020 [Общий семинар, 16:30, online] В.Н. Гурьянова. "Современные методы классификации одноканальных электрокардиограмм", часть 2.
Abstract
Close
На текущий момент существуют мобильные устройства, которые могут считывать одноканальную ЭКГ в домашних условиях. Эти устройства могут быть использованы для предварительного скрининга различных заболеваний. В данном докладе будет рассказано о различных методах, которые позволяют классифицировать одноканальные мобильные ЭКГ с достаточно высоким качеством. Многие из этих методов и улучшений к ним были предложены впервые автором доклада. В докладе выделены достоинства и недостатки предложенных методов. Стоит отметить, что все рассмотренные методы могут быть обобщены для работы с традиционными ЭКГ.
Ссылка для подключения (connection link): подключиться к трансляции.
23.07.2020 [Общий семинар, 16:30, online] В.Н. Гурьянова. "Современные методы классификации одноканальных электрокардиограмм".
Abstract
Close
На текущий момент существуют мобильные устройства, которые могут считывать одноканальную ЭКГ в домашних условиях. Эти устройства могут быть использованы для предварительного скрининга различных заболеваний. В данном докладе будет рассказано о различных методах, которые позволяют классифицировать одноканальные мобильные ЭКГ с достаточно высоким качеством. Многие из этих методов и улучшений к ним были предложены впервые автором доклада. В докладе выделены достоинства и недостатки предложенных методов. Стоит отметить, что все рассмотренные методы могут быть обобщены для работы с традиционными ЭКГ.
Ссылка для подключения (connection link): подключиться к трансляции.
Презентация доклада: скачать.
09.07.2020 [Общий семинар, 16:30, online] А.П. Чупахин. "Исследование гемодинамики головного мозга на основе интраоперационного мониторинга и математических моделей сложных сред", часть 2 (соавторы: А.А. Черевко, А.К. Хе, Д.В. Паршин).
Abstract
Close
Мы расскажем о наших мультидисциплинарных исследованиях жидких сред и тканей мозга: интраоперационный мониторинг кровотока, лабораторное и клиническое моделирование течений крови и тканей мозга, математическое и компьютерное моделирование потоков и тканей в мозге
Ссылка для подключения (connection link): подключиться к трансляции.
Презентация доклада: скачать.
02.07.2020 [Общий семинар, 16:30, online] А.П. Чупахин. "Исследование гемодинамики головного мозга на основе интраоперационного мониторинга и математических моделей сложных сред" (соавторы: А.А. Черевко, А.К. Хе, Д.В. Паршин).
Abstract
Close
Мы расскажем о наших мультидисциплинарных исследованиях жидких сред и тканей мозга: интраоперационный мониторинг кровотока, лабораторное и клиническое моделирование течений крови и тканей мозга, математическое и компьютерное моделирование потоков и тканей в мозге
Ссылка для подключения (connection link): подключиться к трансляции.
Презентация доклада: скачать.
18.06.2020 [Общий семинар, 16:30, online] А.В. Беляев. "Компьютерное моделирование механохимической роли фактора Виллебранда в первичном гемостазе".
Abstract
Close
На первой стадии гемостатических и тромботических процессов в артериях и микрососудах тромбоциты прикрепляются к поврежденной поверхности с помощью белка плазмы крови - фактора фон Виллебранда (VWF). Эта начальная агрегация тромбоцитов обеспечивает основу для дальнейшего роста тромба, биохимических реакций свертывания плазмы крови и остановки кровотечения. В настоящей работе использован принцип многомасштабного моделирования для проверки ряда гипотез относительно взаимосвязи механо-химических свойств VWF и его иерархической молекулярной структуры. Разработан комплекс компьютерных моделей, описывающих динамику мультимеров VWF в гидродинамическом потоке вязкой жидкости с помощью комбинации метода молекулярной динамики и метода решеточных уравнений Больцмана. Было показано, что важнейшим параметром, определяющим поведение модели, является контурная длина мультимера: чем больше димеров в составе макромолекулы, тем при меньших сдвиговых напряжениях активируется адгезия VWF к тромбоцитам. Также показано, что для активации прикрепленного к стенке белка требуется значительно меньшее напряжение сдвига (меньшая скорость потока крови), чем для свободного. Работа выполнена при поддержке РФФИ (19-02-00480 , 19-31-70002), РНФ (17-71-10150) и программы 5-100 (РУДН).
Ссылка для подключения (connection link): подключиться к трансляции.
Презентация доклада: скачать.
11.06.2020 [Общий семинар, 16:30, online] В.А. Вольперт. "Развитие вирусной инфекции с учетом пространственного распределения и распределения вируса по генотипу (продолжение)".
Abstract
Close
Мы рассмотрим модель, описывающую распространение вирусной инфекции в ткани организма с учетом распределения вируса по генотипу. Будет показано, как распределение генотипа вируса, исходная вирусная нагрузка, сила иммунного ответа и наличие иммунитета определяют выбор между легкой и тяжелой формой инфекции.
Ссылка для подключения (connection link): подключиться к трансляции.
Презентация доклада: скачать.
04.06.2020 [Общий семинар, 16:30, online] В.А. Вольперт. "Развитие вирусной инфекции с учетом пространственного распределения и распределения вируса по генотипу".
Abstract
Close
Мы рассмотрим модель, описывающую распространение вирусной инфекции в ткани организма с учетом распределения вируса по генотипу. Будет показано, как распределение генотипа вируса, исходная вирусная нагрузка, сила иммунного ответа и наличие иммунитета определяют выбор между легкой и тяжелой формой инфекции.
Ссылка для подключения (connection link): подключиться к трансляции.
Презентация доклада: доклада: скачать.
21.05.2020 [Общий семинар, 16:30, online] С.И. Мухин. "Моделирование особенностей кровотока при портальной гипертензии".
Abstract
Close
Данный цикл исследований направлен на изучение принципиальных особенностей перераспределения кровотока при таком заболевании методами математического моделирования. Рассматривается квазиодномерная математическая модель кровотока в замкнутой сердечно-сосудистой системе с детализированной системой кровообращения печени. Приведены результаты численных экспериментов исследования кровотока в норме, при различных степенях утраты функционального объема паренхимы печени, как с учётом взаимного влияния кровотока через другие внутренние органы, так и при типичных хирургических вмешательствах.
Ссылка для подключения (connection link): подключиться к трансляции.
Презентация доклада: скачать.
14.05.2020 [Общий семинар, 16:30, online] Н.П. Аносова. "Нейронные сети как математические модели и их использование".
Abstract
Close
Ссылка для подключения (connection link): подключиться к трансляции.
23.04.2020 [Общий семинар, 16:30, online] С.С. Симаков. "Мат. мод. сердечно-сосудистой системы и приложение к мед. задачам".
Abstract
Close
Ссылка для подключения (connection link): подключиться к трансляции.
Презентация доклада: скачать.
23.04.2020 [Аспирантский семинар, 15:00, online] В.А. Вольперт. "Эпидемия коронавируса: текущее состояние и моделирование".
16.04.2020 [Общий семинар, 15:00, online] Я.М. Карандашев. "Моделирование моноантиангиогенной терапии солидных опухолей с различными типами роста".
Abstract
Close
09.04.2020 [Общий семинар, 16:30, online] Я.М. Карандашев. "Нейросети: архитектуры и возможности глубокого обучения".
Abstract
Close
Ссылка для подключения (connection link): подключиться к трансляции.
Материалы семинара доступны по ссылке: материалы.
09.04.2020 [Аспирантский семинар, 15:00, online] Ф.А. Сёмин. "Персонализированное моделирование сердечной функции: проблемы и методы".
02.04.2020 [Общий семинар, 16:30, online] Р.С. Савинков. "Сеть фибробластных ретикулярных клеток в лимфатическом узле. Формирование, функции и свойства".
Abstract
Close
Ссылка для подключения (connection link): подключиться к трансляции.
12.03.2020 [Общий семинар, 16:30, ауд. 558] Ф.А. Сёмин. "Электромеханическая модель сердечной ткани с механо-электрической обратной связью".
Abstract
Close
Для более глубокого понимания причин возникновения и условий существования аритмий, а также для построения точных персонифицированных моделей, которые возможно было бы применить в медицинской практике, необходима детальная модель электромеханики миокарда. Такая модель должна учитывать упомянутые выше взаимосвязи процессов различной природы, и, по возможности, обладать простотой с вычислительной точки зрения. В докладе представлен прототип электромеханической модели миокарда, в которой описание электрической активации сердечной мышцы простой моделью Алиева-Панфилова сопряжено с новой моделью механики миокарда, разработанной коллективом автора доклада. Показаны результаты моделирования возникновения и распространения спиральных волн потенциала действия в деформируемом миокарде. Продемонстрированы эффекты учёта в модели механо-электрической обратной связи, введённые на уровнях клетки и ткани.
06.02.2020 [Аспирантский семинар, 15:00, ауд. 480] Р.С. Савинков. "Алгоритмы построения сетей фибробластных ретикулярных клеток".
Abstract
Close
05.03.2020 [Общий семинар, 16:30, ауд. 550] В.А. Вольперт. "Модели нейронного поля и стимуляция мозга".
Abstract
Close
электрического потенциала в коре головного мозга.
27.02.2020 [Открытый семинар, 16:30] И.Л. Куценко. "Реляционные базы данных. Язык запросов SQL."
Abstract
Close
06.02.2020 [Аспирантский семинар, 15:00] Кристина Леон. "Математическая модель сосуществования вирусов в пространстве генотипов".
16.05.2019 В.А. Вольперт. "Реакционно-диффузионные волны и их приложения".
Abstract
Close
25.04.2019 Ф.А. Сёмин. "Применение модели сердечной мышцы для исследования влияния сократительных и регуляторных характеристик миокарда на производительность сердца".
Abstract
Close
В докладе представлена модель сердечно-сосудистой системы, в которой левый желудочек сердца с осесимметричной аппроксимацией описывали многомасштабной моделью, включающей новую кинетическую модель механики сердечной мышцы. Приведены результаты численных экспериментов с параметрами модели, соответствующими некоторым типам наследственных кардиомиопатий, приводящим к патологическим изменениям в работе сократительных и регуляторных белков сердечной мышцы. Показаны эффекты таких патологий на производительность сердца.
18.04.2019 А.А. Токарев. "Взаимосвязь между скоростью и амплитудой автоволны в модели Грея-Скотта в изолированной системе".
Abstract
Close
11.04.2019 Н.В. Перцев. "Простейшая компартментная модель динамики ВИЧ-1 инфекции".
Abstract
Close
28.03.2019 Г.Т. Гурия. "Активная коррекция гемостаза на основании ультразвукового мониторинга процессов смены кровью агрегатного состояния".
Abstract
Close
В лаборатории математического моделирования биологических процессов НМИЦ Гематологии Минздрава России, был разработан новый экспериментальный стенд, предоставляющий возможность валидировать некоторые результаты математического моделирования. В его основе лежит замкнутая система трубок, наполненных плазмой крови или же цельной кровью. Благодаря перистальтическому насосу в системе могут создаваться различные режимы течения в широком диапазоне скоростей. Такая конструкция позволила сосредоточиться, прежде всего, на свойствах самой крови, а не сосудов, сердца или иного её окружения.
За агрегатным состоянием текущей крови велось непрерывное наблюдение посредством ультразвукового допплеровского метода. Появление в потоке крови микросгустков фибрина после начала свертывания приводило к значительному, в 5-6 раз, увеличению интенсивности отраженного сигнала. Такой резкий рост легко фиксировался и служил индикатором начала процессов свертывания крови. За счет специально собранного автоматического инжектора стало возможным вводить в систему фибринолитический препарат, растворяющий тромбы, во-первых, каждый раз строго воспроизводимым образом, и, во-вторых, в течение 10 первых секунд после регистрации начала свертывания.
В ходе экспериментов было показано, что фармакологическое воздействие на таких ранних стадиях свертывания может приводить к быстрому и полному растворению формирующихся в потоке тромбов. Образования крупных тромбов, способных перекрыть кровоток, при этом удается избежать. Таким образом, была реализована схема активного контроля работы системы свертывания: в ответ на ее стремительную запороговую динамику своевременно вводился препарат, запускающий обратные процессы.
Развитый подход может быть использован в текущем виде не только для валидации моделей образования и растворения фибриновых сгустков, но и для испытаний препаратов фибринолитического класса, служащих для растворения тромбов в клинике. С его помощью можно так же сравнивать эффективность уже существующих препаратов и разрабатывать новые протоколы их применения. В будущем же открываются перспективы для создания нового класса устройств, носимых на теле или же вживляемых, для автоматической коррекции возникающих тромбозов.
14.03.2019 Р.С. Савинков. "Разработка ПО для моделирования индивидуальной клеточной динамики".
Abstract
Close
Для некоторых задач, исследователями были разработаны узконаправленные модели, позволившие учитывать динамику клеток в глобальном иммунном процессе, но существенная доля задач математического моделирования в иммунологии всё ещё не может быть исследована с подобной тщательностью. Для частичного решения этой проблемы, было разработано программное обеспечение, позволяющее охватить широкий спектр задач, связанных с моделированием пространственной динамики процессов, происходящих в областях с активными межклеточными взаимодействиями в двумерном и трёхмерном случаях.
Разработанное ПО может быть гибко настроено для моделирования произвольного количества типов клеток с различными вариантами взаимодействия как между клетками, так и взаимодействия клеток с веществами, находящимися в окружающей среде. Решение выполнено на языке С++ с учётом возможности акселерации решения на графических процессорах, что существенно ускоряет любые расчёты, связанные с реакционно-диффузионными процессами внутри расчётной области и может быть применено в операционных системах Linux и Windows.
28.02.2019 А.К. Цатурян. "Механические аспекты кальциевой регуляции мышечного сокращения в норме и при патологии".
Abstract
Close
17.01.2019 И.Б. Коваленко. "Суперкомпьютерное моделирование в биологии и медицине".
Abstract
Close
20.12.2018 В.А. Вольперт. "Пространственные модели развития инфекции и иммунного ответа (третий семинар тематического цикла)".
Abstract
Close
13.12.2018 В.А. Вольперт. "Дарвиновская эволюция: биологические виды, клетки и вирусы (второй семинар тематического цикла)".
Abstract
Close
06.12.2018 В.А. Вольперт. "Математическое моделирование сердечно-сосудистых заболеваний (первый семинар тематического цикла)".
Abstract
Close
15.11.2018 С.Ю. Коваленко. "Задачи поиска оптимальной терапии в математических моделях глиом".
Abstract
Close
В докладе будет рассказано о методах решения задач оптимального управления на примере различных математических моделей терапии. А также подробно будет разобрана задача выживаемости, в которой фазовые ограничения очерчивают некоторую область в пространстве показателей состояния пациента. Задача выживаемости состоит в максимизации времени жизни пациента, поиск ведется именно таких стратегий лечения, которые возвращают показатели в исходное положение (и мы видим на графиках периодические траектории). Периодические траектории говорят о том, что смертельно опасная болезнь переведена в разряд хронических.
01.11.2018 Д.С. Гребенников. "Математические модели подвижности клеток иммунной системы".
Abstract
Close
В докладе будет рассказано о механизмах и имеющихся математических моделях подвижности основных типов иммунных клеток. Движение клеток определяется стохастическими силами внутренней подвижности, регулируемой реорганизацией цитоскелета и мембраны клетки, а также вязкоэластичным взаимодействием с другими клетками среды. Внутренняя подвижность может регулироваться механическими и химическими сигналами от внеклеточного матрикса и хемокинов (контактное ингибирование перемещения, гаптотаксис, хемотаксис). Механизмы подвижности фибробластных клеток позволяют реорганизовывать коллагеновую структуру внеклеточного матрикса и формировать стромальный каркас лимфоузла. Напротив, активная внутренняя подвижность лимфоцитов и дендритных клеток позволяет адаптивно менять свою форму и направление, не меняя структуры внеклеточного матрикса. Благодаря механизмам гаптотаксиса и хемотаксиса, лимфоциты могут направленно перемещаться вдоль стромальной сети к АПК. Стабильный иммунологический синапс между АПК и специфическими лимфоцитами образуется за счет сильных специфических сил межклеточной адгезии по сравнению с неспецифическими. Имеющиеся модели подвижности иммунных клеток варьируются от детального описания механизмов подвижности одной клетки до феноменологического непрерывного описания клеточной среды. Мезомасштабные модели позволяют описать коллективное движение иммунных клеток, воспроизводя при этом ключевые механизмы подвижности.
18.10.2018 Р.С. Савинков. "Построение трёхмерных геометрических моделей элементов лимфатического узла".
Abstract
Close
04.10.2018 А.А. Полежаев. "Сложные пространственно-временные структуры в биологических и химических системах и механизмы их образования".
Abstract
Close
В первой части доклада будет кратко рассказано об экспериментальном изучении структур в химических системах и об имеющихся теоретических подходах к объяснению механизмов их возникновения. Некоторые структуры, такие как автоволны и стационарные неоднородные (диссипативные) структуры, уже нашли адекватное объяснение и могут быть описаны относительно простыми математическими моделями, другие же требуют разработки более сложных подходов. На примере трёх экспериментально наблюдаемых структур – сегментированных волн и осциллонов (уединённых автоволновых структур) в двумерной химической среде, а также спиральных и кольцевых волн на фронте распространяющейся реакции (напр., горения) в трёхмерном случае – будет продемонстрировано, что адекватным подходом к моделированию таких систем является построение блочных моделей, отражающих их иерархическую организацию.
27.09.2018 Andreas Meyerhans. "Fundamental decisions in the virus-infected host".
Abstract
Close
To identify the essential features in the virus–immune system´s crosstalk that ultimately decides an infection fate, as well as to understand mechanistic relationships between immune responses and virus control in the chronic infection phase, we used the infection of mice with the non-cytopathic Lymphocytic Choriomeningitis Virus (LCMV). Time-series transcriptomes from spleens of acute and chronic LCMV-infected mice were analyzed by weighted gene co-expression network analysis (WGCNA) and related to virus loads and immune responses. We could identify modules of highly connected genes (hub genes) that represent the main biological pathways involved in acute versus persistent infection outcomes. Virus-specific CD8 T cell exhaustion during persistent LCMV infection is followed by an increase of crosspresenting Xcr1+DC in spleen that maintain a low level of cytotoxic effector cells and control virus loads to non-pathogenic levels. Thus, immunotherapeutic strategies to boost Xcr1+DC-dependent T cell responses may present a mean to better control virus loads in chronic virus infections.
Reference:
Jordi Argilaguet, Mireia Pedragosa, Anna Esteve-Codina, Graciela Riera, Enric Vidal, Cristina Peligero-Cruz, David Andreu, Tsuneyasu Kaisho, Gennady Bocharov, Burkhard Ludewig, Simon Heath and Andreas Meyerhans. Systems analysis reveals complex biological processes in virus infection fate decisions (submitted).
20.09.2018 Г.А. Бочаров. "Современные подходы к математическому моделированию иммунных процессов".
Abstract
Close
13.09.2018 Ф.А. Семин. "Многомасштабное моделирование сердечного сокращения".
Abstract
Close
28.06.2018 М. Кузнецов. "Математическое моделирование роста злокачественной опухоли и антиангиогенной терапии".
21.06.2018 А. Беляев, А. Токарев. "Гемостаз и тромбоз: биологические основы и подходы к моделированию".
- Hits: 11947
